Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

vweight — возвращает веса вершин;

isplanar — упрощает граф, удаляя циклы и повторяющиеся ребра, и проверяет его на планарность (возвращает true, если граф оказался планарным и false в противном случае).

Функции с типовыми возможностями графов:

flow — находит максимальный поток в сети от одной заданной вершины к другой;

shortpathtree — находит кратчайший путь в графе с помощью алгоритма Дейкстры.

Каждая из этих команд имеет одну или несколько синтаксических форм записи. Их можно уточнить с помощью справочной системы. С ее помощью можно ознакомиться и с назначением других функций этого обширного пакета. Проиллюстрируем его применение на нескольких типичных примерах.

На рис. 9.8 показан пример создания графа, имеющего четыре вершины, и графа Петерсона с выводом их графиков графической функцией draw.

Рис. 9.8. Построение графов

На рис. 9.9 показан другой пример работы с графами — построение графа функцией complete и затем его преобразование путем удаления части вершин. Исходный и преобразованный графы строятся функцией draw.

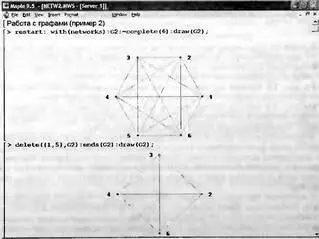
Рис. 9.9. Преобразование графа удалением части вершин

В третьем примере (рис. 9.10) граф формируется по частям — вначале задается пустой граф функцией new, а затем с помощью функций addvertex и addedge в него включаются вершины и ребра. Далее функция connect соединяет вершину a с вершиной с, делая граф замкнутым. Функция draw строит сформированный таким образом граф, а функции head и tail используются для выявления «голов» и «хвостов» графа.

Рис. 9.10. Формирование графа и определение его «голов» и «хвостов»

В четвертом примере, представленном на рис. 9.11, показано создание графа G2 (его изображение было приведено на рис. 9.9) с вычислением для этого графа максимального потока от вершины 1. Обратите внимание, что в параметрах функции flow, использованной для этого, заданы две переменные: eset — принимает значение множества с ребрами, по которым проходит максимальный поток, и comp — принимает значение множества, в котором содержатся вершины , по которым проходит максимальный поток. Значения этих переменных выведены в области вывода. В заключительной части этого примера показано применение функции shortpathtree, ищущей наиболее короткий путь от вершины 1 до других вершин.

Рис. 9.11. Пример вычисления максимального потока и наиболее коротких путей для заданного графа

Приведенный ниже еще один пример иллюстрирует работу функции show, выдающей таблицу с полной информацией о графе, созданном функцией complete:

> restart:with(networks):G2:=complete(4):

> show(G2);

Разумеется, приведенные примеры далеко не исчерпывают всех задач, которые можно решать с применением графов. Но они наглядно демонстрируют, что для большинства пользователей пакет networks превращает графы из окутанного ореолом таинственности модного средства в простой рабочий инструмент.

Этот пакет полезен математикам, часто использующим рекуррентные отношения и формулы. Он дополняет функцию rsolve основной библиотеки и содержит следующие функции:

> with(LREtools);

В пакете дифференциальных форм содержится следующий ряд функций: