Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

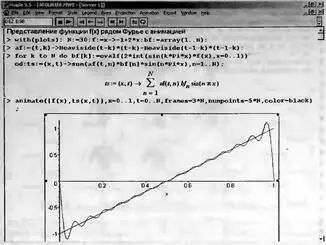
Рис. 8.67. Второй (завершающий) кадр анимации

Для f(x) = 1 строится приближение для однополярного импульса с длительностью 1 и амплитудой 1, при f(x)=x приближение для пилообразного линейно нарастающего импульса, при f(x)=x^2 — приближение для нарастающего по параболе импульса, при f(x) = signum(x-1/2) — приближение для симметричного прямоугольного импульса — меандра и т.д. Фактически можно наблюдать анимационную картину изменения формы импульса по мере увеличения числа используемых для синтеза гармоник. Выбор используемого числа гармоник осуществляет амплитудный селектор — функция af(t, k), основанная на применении функции Хевисайда.

Самым интересным в этом примере оказывается наблюдение за зарождением и эволюцией эффекта Гиббса — так называют волнообразные колебания на вершине импульса, связанные с ограничением числа гармоник при синтезе сигнала. С ростом числа гармоник эффект Гиббса не исчезает, просто обусловленные им выбросы вблизи разрывов импульса становятся более кратковременными. Амплитуда импульсов может достигать 9% от амплитуды перепадов сигнала, что сильно ухудшает приближение импульсных сигналов рядами Фурье и вынуждает математиков разрабатывать особые меры по уменьшению эффекта Гиббса.

Можно ли наблюдать одновременно все фазы анимации? Можно! Для этого достаточно оформить анимационную картину, созданную функцией animate, в виде отдельного графического объекта, например, g, после чего можно вывести все его фазы оператором display. Это и иллюстрирует рис. 8.68. На этот раз задано f(x)=signum(x-1/2) и N=25. Таким образом, рассматриваются симметричные прямоугольные импульсы — меандр. У каждого рисунка координатные оси с делениями удалены параметром axes=none.

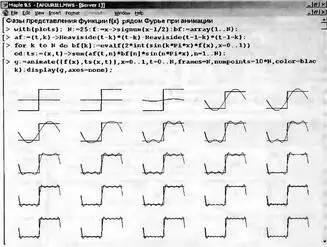
Рис. 8.68. Иллюстрация получения всех кадров анимации двумерного графика

Любопытно отметить, что при определенных числах гармоник связанная с колебательными процессами неравномерность вершины импульса резко уменьшается. Наблюдение этого явления и является наиболее интересным и поучительным при просмотре данного примера.

При внимательном просмотре рис. 8.68 заметно, что, после некоторого периода установления, фазы анимационной картинки практически повторяются. Это связано с известным обстоятельством — установившийся спектр меандра содержит только нечетные гармоники. Поэтому, к примеру, вид спектрального разложения при 22 гармониках будет тот же, что и при 21 гармонике, при 24 гармониках тот же, что при 23 и т.д. Однако, эта закономерность проявляется только при установившемся (стационарном) спектре.

Наблюдение за развитием поверхности производит на многих (особенно на студентов) большое впечатление. Оно позволяет понять детали создания сложных трехмерных графиков и наглядно представить их математическую сущность.

Как и для случая анимации двумерного графика, большой интерес представляет построение всех фаз анимации на одном рисунке. Делается это точно так же, как в двумерном случае. Это иллюстрирует рис. 8.69. На нем представлены 8 фаз анимации трехмерной поверхности cos(f*x*y/3), представленной функцией трех переменных t, х и у. При этом изменение первой переменной создает фазы анимации поверхности.

Рис. 8.69. Фазы анимации трехмерной поверхности

Применение анимации дает повышенную степень визуализации решении ряда задач, связанных с построением двумерных и трехмерных графиков. Следует отметить, что построение анимированных графиков требует дополнительных и достаточно существенных затрат оперативной памяти. Поэтому злоупотреблять числом стоп-кадров таких графиков не стоит.

Наряду с описанной выше формой применения функций анимации animate и animate3d возможны и иные формы их применения. Ограничимся парой примеров такого применения. В приведенном ниже примере анимация импликативного графика заключается в превращении окружности в наклонный эллипс: