Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

> with(plots) :

plots[animate](implicitplot, [х^2+А*х*y+y^2=2, x=-2..2, y=-2..2,

grid=[50,50]], A=0..1, frames=25);

Для этого задано 25 кадров (фреймов) изменения параметра А от 0 до 1. В другом примере анимация задает деформацию мембраны в виде квадрата с жестко закрепленными границами:

> plots[animate](plot3d, [sin(А)*ехр(-х^2-y^2), х=-2..2, y=-2..2],

А=0..2*Pi);

Ввиду очевидности этих примеров графики результатов их выполнения не приводятся — пользователь может просмотреть их самостоятельно.

Иногда возникает необходимость сменить координаты к какого-то графика или изменить масштаб по определенной оси. Первая задача может несколько озадачить пользователя. Однако она легко решается средствами графики пакета stats — см. примеры на рис. 8.70. Масштабирование и сдвиг решаются проще — введением масштабных коэффициентов и констант сдвига. Но и эти задачи еще проще решаются указанными выше средствами графики.

Рис. 8.70. Примеры смены координат и масштабирования графиков

В первом примере рис. 8.70 используется функция xyexchange(p) меняющая оси у графического объекта р. Во втором случае используется функция xscale(k,p) масштабирующая объект по оси х в k раз. А в третьем примере используется функция сдвига объекта xshift(xs,p) на расстояние xs и масштабирования zscale(k,p) в k раз по оси z. О других функциях подпакета статистической графики можно судить по названиям его функций.

В пакет plots была введена новая функция построения стрелок в пространстве arrow. Она задается в виде:

arrow(u,[v,]opts)

или

arrow(U,opts)

Построение стрелок задается по одномерными массивами координат начала стрелок и их направления u и v или двумерным массивом U, которые могут быть представлены векторами, списками или множествами. Вид стрелок задается параметром opts, который может иметь значения shape, length, width, head_width, head_length или plane и задает вид стрелок (форму, длину, ширину и т.д.). Детали задания параметров можно найти в справке по данной функции. Рис. 8.71 дает наглядное представление о ее возможностях.

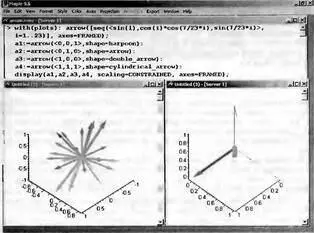
Рис. 8.71. Построение стрелок с помощью функции arrow

Maple 9.5 позволяет строить достаточно сложные комбинированные графики, содержащие различные графические и текстовые объекты. Пример построения такого графика представлен на рис. 8.72.

Рис. 8.72. Пример построения сложного объекта, состоящего из 8 графических и текстовых объектов

Представленный на рис. 8.72 объект задает построение восьми графических объектов от р1 до р8. Среди них цилиндр, две пересекающие его плоскости и иные (в том числе текстовые) объекты. Обратите внимание на способ вывода этих объектов функцией display3d. Этот пример показывает, что с помощью графических программных средств Maple 9 можно строить достаточно замысловатые графики, которые могут использоваться для визуализации тех или иных геометрических и иных объектов.

Дифференциальные параметры функции f(x), описывающей некоторую кривую, имеют большое значение для анализа ее особых точек и областей существования. Так, точки с нулевой первой производной задают области, где кривая нарастает (первая производная положительна) или убывает (первая производная отрицательна) с ростом аргумента х. Нули второй производной задают точки перегиба кривой.

Для такого анализа особенно удобен новый пакет Calculus 1, включенный в пакет расширения Student. На рис. 8.73. показано применение функции FunctionChart для визуализации дифференциальных параметров кривой, которая представляет собой сложную функцию. По умолчанию анализ ведется в интервале изменения х от -10 до +10. Экстремальные точки помечаются ромбиком, точки перегиба крестиком, нули кружочками, а области кривых — заливкой цветом.