Michel Anders - Написание скриптов для Blender 2.49

Скрипт orbit.py , который мы разработаем, будет предпринимать следующие шаги:

1. Определение точки середины пути между выбранными объектами.

2. Определение протяженности выбранных объектов.

3. Определение IPO для объекта один.

4. Определение IPO для объекта два.

Определение точки середины пути между выбранными объектами будет достаточно легко: мы просто возьмем среднее позиций обоих объектов. Определение протяженности выбранных объектов будет всё-таки некоторым вызовом. Объект может иметь неправильную форму, и определение кратчайшего расстояния с учётом любого возможного поворота объектов на пути трудно для вычисления. К счастью, мы можем сделать разумное приближение, так как каждый объект имеет связанный с ним габаритный ящик (bounding box).

Этот габаритный ящик является прямоугольным параллелепипедом, который просто включает в себя все точки объекта. Если взять половину диагонали в качестве протяженности (размера) объекта, то легко видеть, что это расстояние может быть гораздо больше того, насколько близко мы можем быть к другому объекту, не касаясь его, в зависимости от точной формы объекта. Но это гарантирует, что мы никогда не окажемся слишком близко. Этот габаритный ящик легко получить из объектного метода getBoundBox() в виде списка из восьми векторов, каждый из которых представляет один из углов габаритного ящика. Понятие проиллюстрировано на следующем рисунке, где показаны габаритные ящики двух сфер:

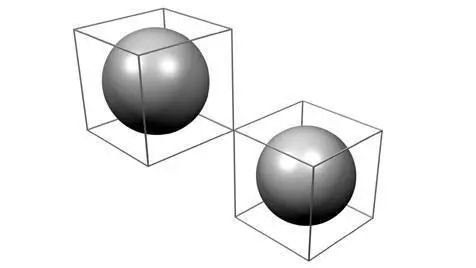
Длина диагонали габаритного ящика может быть вычислена определением как максимального так и минимального значений для каждой из координат x, y, и z. Компоненты вектора, представляющего эту диагональ, являются разницами между этими максимумом и минимумом. Длина диагонали впоследствии получается взятием квадратного корня суммы квадратов компонент x, y, и z. Функция diagonal() довольно кратко реализована, так как она использует много встроенных функций Питона. Она принимает список векторов в виде аргумента, а затем проходит циклом по каждой из компонент (выделено. Компоненты x, y, и z объекта Vector в Блендере могут быть доступны по индексам 0, 1, и 2 соответственно):

def diagonal(bb):

maxco=[]

minco=[]

for i in range(3):

maxco.append(max(b[i] for b in bb))

minco.append(min(b[i] for b in bb))

return sqrt(sum((a-b)**2 for a,b in zip(maxco,minco)))

Она определяет пределы для каждой компоненты, используя встроенные функции max() и min() . В конце она возвращает длину, спаривая каждый минимум и максимум с помощью функции zip() .

Следующим шагом нужно проверить, что мы имеем в точности два выбранных объекта, и если это не так, сообщить пользователю, отображая всплывающее меню (выделено в следующем куске кода). Если у нас есть два выбранных объекта, мы извлекаем их позиции и габаритные ящики. Затем мы вычисляем максимальное расстояние w , на которое каждый объект должен отклониться от своего пути, оно должно быть половиной минимального расстояния между ними, что эквивалентно четверти суммы длин диагоналей этих объектов:

obs=Blender.Scene.GetCurrent().objects.selected

if len(obs)!=2:

Draw.PupMenu('Please select 2 objects%t|Ok')

else:

loc0 = obs[0].getLocation()

loc1 = obs[1].getLocation()

bb0 = obs[0].getBoundBox()

bb1 = obs[1].getBoundBox()

w = (diagonal(bb0)+diagonal(bb1))/4.0

Прежде, чем мы сможем вычислить траектории обоих объектов, мы сначала создадим два новых и пустых объекта кривых IPO:

ipo0 = Ipo.New('Object','ObjectIpo0')

ipo1 = Ipo.New('Object','ObjectIpo1')

Мы произвольно выбираем начальный и конечный кадры нашей операции обмена в 1 и 30 соответственно, но скрипт легко может быть адаптирован для того, чтобы пользователь вводил эти величины. Мы итерируем по каждой отдельной кривой IPO для IPO местоположения и создаем первую точку (или ключевой кадр) и этим самым фактически назначается кортеж (номер кадра, значение) на кривую (выделенные строки следующего кода). Последующие точки могут быть добавлены к этим кривым по индексу - их номеру кадра присвоением значения, как это сделано для кадра 30 в следующем коде:

for i,icu in enumerate((Ipo.OB_LOCX,

Ipo.OB_LOCY,Ipo.OB_LOCZ)):

ipo0[icu]=(1,loc0[i])

ipo0[icu][30]=loc1[i]

ipo1[icu]=(1,loc1[i])

ipo1[icu][30]=loc0[i]

ipo0[icu].interpolation =

IpoCurve.InterpTypes.BEZIER

ipo1[icu].interpolation =