Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]

многократного использования промежуточных результатов называется мемоизацией . Он повышает производительность функции fib:

Очевидно, что в дереве рекурсивных вызовов для задачи о рюкзаке (см. рис. 3.13) имеются многократно повторяемые вызовы. Применение того же самого приема, который мы использовали для функции Фибоначчи, позволяет избежать этих повторных вызовов и в итоге уменьшить объем вычислений (рис. 3.15).

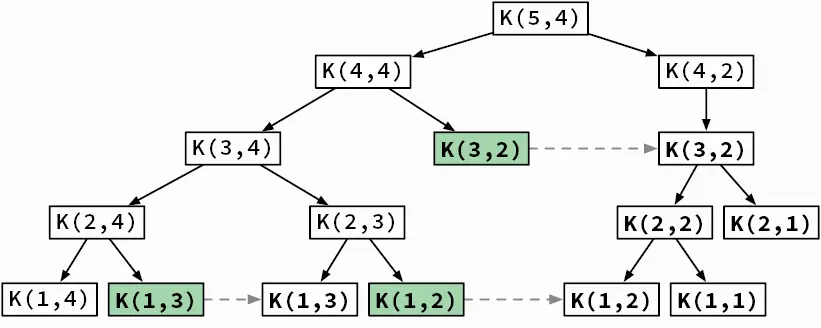
Рис. 3.15.Рекурсивное решение задачи о рюкзаке при помощи мемоизации

Динамическое программирование позволяет добиться от чрезвычайно медленного программного кода приемлемого быстродействия. Тщательно анализируйте свои алгоритмы, чтобы убедиться, что в них нет повторных вычислений. Как мы увидим далее, иногда перекрывающиеся подзадачи могут порождать проблемы.

Дерево рекурсии для функции trade (см. рис. 3.12) не имеет повторных вызовов, и все равно делает повторные вычисления. Он просматривает вход, чтобы найти максимальное и минимальное значения. Затем входные данные разбиваются на две части, и рекурсивные вызовы анализируют их снова, чтобы найти максимум и минимум в каждой половине [42] Вам нужно найти самого высокого мужчину, самую высокую женщину и самого высокого человека в комнате. Будете ли вы измерять рост каждого присутствующего с целью найти самого высокого человека, а затем делать это еще и еще раз применительно к женщинам и мужчинам по отдельности? . Нам нужен другой принцип, для того чтобы избежать этих повторных проходов.

До сих пор мы использовали нисходящий подход, где объем входных данных постепенно уменьшается, пока не будут достигнуты базовые случаи. Но мы также можем пойти снизу вверх : сначала вычислить базовые случаи, а затем раз за разом собирать их, пока не получим общий результат. Давайте решим задачу о лучшей сделке (см. раздел «Полный перебор» ) таким способом.

Пусть P ( n ) — это цена в n -й день, а B ( n ) — лучший день для покупки при продаже в n -й день. Если мы продаем в первый день, то купить у нас получится только тогда же, других вариантов нет, поэтому B (1) = 1. Но если мы продаем во второй день, B (2) может равняться 1 либо 2:

• P (2) < P (1)! B (2) = 2 (купить и продать в день 2);

• P (2) ≥ P (1)! B (2) = 1 (купить в день 1, продать в день 2).

День с самой низкой ценой перед днем 3, но не в день 3 — это B (2). Потому для B (3):

• P (3) < цена в день B (2) —> B (3) = 3.

• P (3) ≥ цена в день B (2) —> B (3) = B (2).

Обратите внимание, что день с самой низкой ценой перед днем 4 будет B (3). Фактически для каждого n день с самой низкой ценой перед днем n — B ( n — 1). Мы можем это использовать, чтобы выразить B ( n) через B ( n — 1):

Когда у нас есть все пары [ n, B ( n )] для для каждого дня n , решением является пара, которая дает самую высокую прибыль. Следующий алгоритм решает задачу, вычисляя все значения B снизу вверх:

function trade_dp(P)

····B[1] ← 1

····sell_day ← 1

····best_profit ← 0

····for each n from 2 to P.length

········if P[n] < P[B[n-1]]

············B[n] ← n

········else

············B[n] ← B[n-1]

········profit ← P[n] — P[B[n]]

········if profit > best_profit

············sell_day ← n

············best_profit ← profit

····return (sell_day, B[sell_day])

Алгоритм выполняет фиксированное число простых операций для каждого элемента входного списка, следовательно, он имеет сложность O ( n). Это огромный рывок в производительности по сравнению со сложностью предыдущего алгоритма O ( n log n) — и совершенно несравнимо со сложностью O ( n 2 ) метода полного перебора. Этот алгоритм также имеет пространственную сложность O ( n) , поскольку вспомогательный вектор B содержит столько же элементов, что и входные данные. Из приложения IV вы узнаете, как сэкономить память за счет создания алгоритма с пространственной сложностью O (1).