Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]

3) лучшая сделка с покупкой в первой половине и продажей во второй.

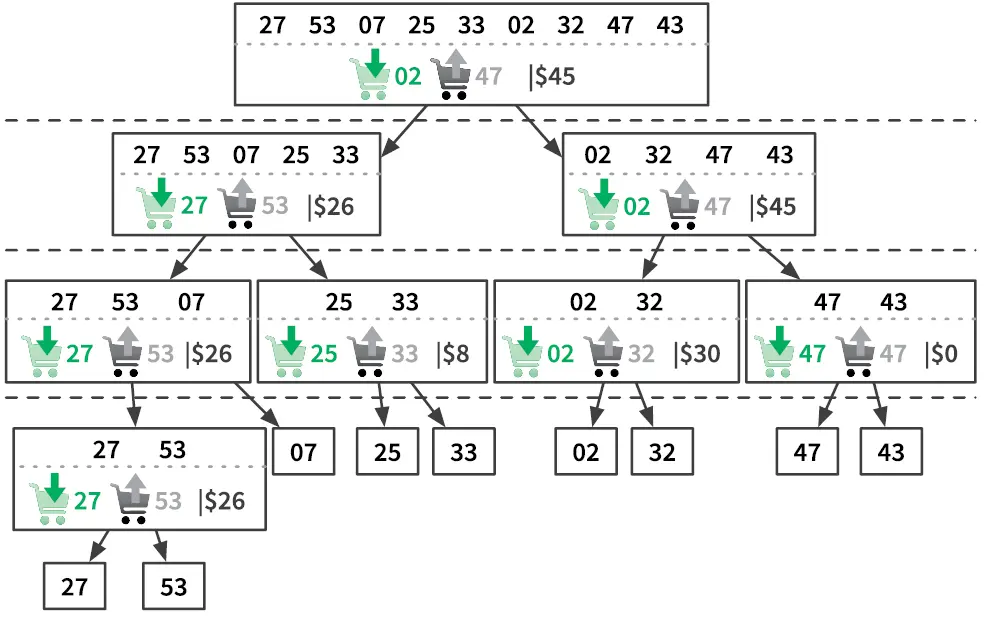
Рис. 3.12.Демонстрация выполнения функции trade. Прямоугольники показывают отдельные вызовы trade с входными и выходными данными

Первые два случая — это решения подзадач. Третий легко находится: нужно найти самую низкую цену в первой половине списка и самую высокую во второй. Если на входе данные всего за один день, то единственным вариантом становится покупка и продажа в этот день, что приводит к нулевой прибыли.

function trade(prices)

····if prices.length = 1

········return 0

····former ← prices.first_half

····latter ← prices.last_half

····case3 ← max(latter) — min(former)

····return max(trade(former), trade(latter), case3)

Функция trade выполняет тривиальное сравнение, разбивает список пополам и находит максимум и минимум в его половинах. Поиск максимума или минимума в списке из n элементов требует просмотра всех n элементов, таким образом, отдельный вызов trade стоит O ( n ).

Вы наверняка заметите, что дерево рекурсивных вызовов функции trade (рис. 3.12) очень похоже на такое же для сортировки слиянием (рис. 3.11). Оно тоже имеет log 2 n шагов разбиения, каждый стоимостью O ( n ). Следовательно, функция trade тоже имеет сложность O ( n log n ) — это огромный шаг вперед по сравнению со сложностью O ( n 2) предыдущего подхода, основанного на полном переборе.

Задачу о рюкзаке (см. раздел «Полный перебор» ) тоже можно разделить и тем самым решить. Если вы не забыли, у нас n предметов на выбор. Мы обозначим свойство каждого из них следующим образом:

• w i— это вес i -го предмета;

• v i— это стоимость i- го предмета.

Индекс i предмета может быть любым числом от 1 до n . Максимальный доход для вместимости c рюкзака с уже выбранными n предметами составляет K ( n, c ). Если рассматривается дополнительный предмет i = n + 1, то он либо повысит, либо не повысит максимально возможный доход, который становится равным большему из двух значений.

1. K ( n, c ) — если дополнительный предмет не выбран.

2. K ( n, c − w n+1) + v n+1— если дополнительный предмет выбран.

Случай 1 предполагает отбраковку нового предмета, случай 2 — включение его в набор и размещение среди выбранных ранее вещей, обеспечивая для него достаточное пространство. Это значит, что мы можем определить решение для n предметов как максимум частных решений для n — 1 предметов:

K ( n, c ) = max ( K ( n − 1, c ),

K ( n − 1, c − w n) + v n).

Вы уже достаточно знаете и должны легко преобразовать эту рекурсивную формулу в рекурсивный алгоритм. Рисунок 3.13 иллюстрирует, как рекурсивный процесс решает задачу. На схеме выделены одинаковые варианты — они представляют идентичные подзадачи, вычисляемые более одного раза. Далее мы узнаем, как предотвратить такие повторные вычисления и повысить производительность.

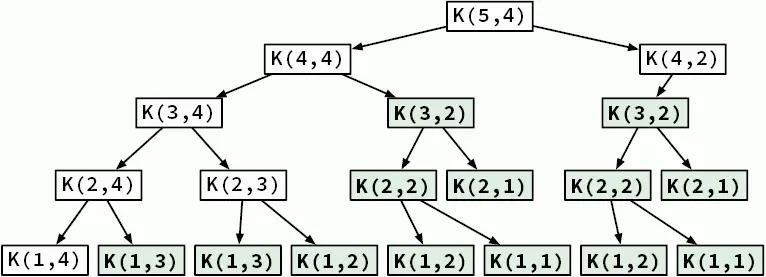
Рис. 3.13.Решение задачи о рюкзаке с 5 предметами и вместимостью рюкзака 4. Предметы под номерами 5 и 4 весят две единицы, остальные — одну единицу

Во время решения задачи иногда приходится выполнять одни и те же вычисления многократно [41] В таком случае говорят, что задачи имеют перекрывающиеся подзадачи. . Динамическое программирование позволяет идентифицировать повторяющиеся подзадачи, чтобы можно было выполнить каждую всего один раз. Общепринятый метод, предназначенный для этого, основан на запоминании и имеет «говорящее» название.

Помните алгоритм вычисления чисел Фибоначчи? Его дерево рекурсивных вызовов (см. рис. 3.3) показывает, что fib(3) вычисляется многократно. Мы можем это исправить, сохраняя результаты по мере их вычисления и делая новые вызовы fib только для тех вычислений, результатов которых еще нет в памяти (рис. 3.14). Этот прием

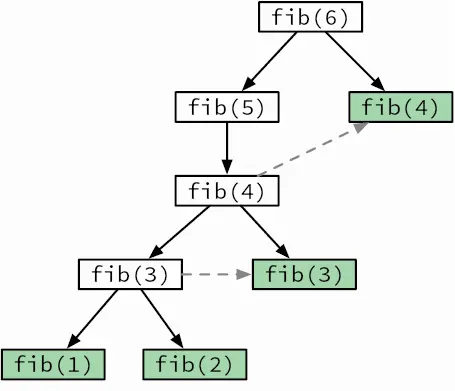
Рис. 3.14.Дерево рекурсивных вызовов для dfib. Зеленые прямоугольники обозначают вызовы, не выполняемые повторно