Брайан Керниган - Язык программирования Си. Издание 3-е, исправленное

};

может потребоваться восемь байтов, а не пять. Оператор sizeof возвращает правильное значение.

Наконец, несколько слов относительно формата программы. Если функция возвращает значение сложного типа, как, например, в нашем случае она возвращает указатель на структуру:

struct key *binsearch(char *word, struct key *tab, int n)

то "высмотреть" имя функции оказывается совсем не просто. В подобных случаях иногда пишут так:

struct key *

binsearch(char *word, struct key *tab, int n)

Какой форме отдать предпочтение - дело вкуса. Выберите ту, которая больше всего вам нравится, и придерживайтесь ее.

Предположим, что мы хотим решить более общую задачу - написать программу, подсчитывающую частоту встречаемости для любых слов входного потока. Так как список слов заранее не известен, мы не можем предварительно упорядочить его и применить бинарный поиск. Было бы неразумно пользоваться и линейным поиском каждого полученного слова, чтобы определять, встречалось оно ранее или нет - в этом случае программа работала бы слишком медленно. (Более точная оценка: время работы такой программы пропорционально квадрату количества слов.) Как можно организовать данные, чтобы эффективно справиться со списком произвольных слов?

Один из способов - постоянно поддерживать упорядоченность уже полученных слов, помещая каждое новое слово в такое место, чтобы не нарушалась имеющаяся упорядоченность. Делать это передвижкой слов в линейном массиве не следует, - хотя бы потому, что указанная процедура тоже слишком долгая. Вместо этого мы воспользуемся структурой данных, называемой бинарным деревом.

В дереве на каждое отдельное слово предусмотрен "узел", который содержит:

- указатель на текст слова;

- счетчик числа встречаемости;

- указатель на левый сыновний узел;

- указатель на правый сыновний узел.

У каждого узла может быть один или два сына, или узел вообще может не иметь сыновей.

Узлы в дереве располагаются так, что по отношению к любому узлу левое поддерево содержит только те слова, которые лексикографически меньше, чем слово данного узла, а правое - слова, которые больше него. Вот как выглядит дерево, построенное для фразы " now is the time for all good men to come to the aid of their party " ("настало время всем добрым людям помочь своей партии"), по завершении процесса, в котором для каждого нового слова в него добавлялся новый узел:

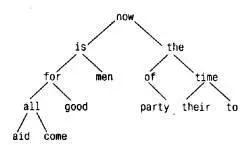
Чтобы определить, помещено ли уже в дерево вновь поступившее слово, начинают с корня, сравнивая это слово со словом из корневого узла. Если они совпали, то ответ на вопрос - положительный. Если новое слово меньше слова из дерева, то поиск продолжается в левом поддереве, если больше, то - в правом. Если же в выбранном направлении поддерева не оказалось, то этого слова в дереве нет, а пустующая позиция, говорящая об отсутствии поддерева, как раз и есть то место, куда нужно "подвесить" узел с новым словом. Описанный процесс по сути рекурсивен, так как поиск в любом узле использует результат поиска в одном из своих сыновних узлов. В соответствии с этим для добавления узла и печати дерева здесь наиболее естественно применить рекурсивные функции.

Вернемся к описанию узла, которое удобно представить в виде структуры с четырьмя компонентами:

struct tnode { /* узел дерева */

char *word; /* указатель на текст */

int count; /* число вхождений */

struct tnode *left; /* левый сын */

struct tnode *right; /* правый сын */

};

Приведенное рекурсивное определение узла может показаться рискованным, но оно правильное. Структура не может включать саму себя, но ведь

struct tnode *left;

объявляет left как указатель на tnode , а не сам tnode .

Иногда возникает потребность во взаимоссылающихся структурах: двух структурах, ссылающихся друг на друга. Прием, позволяющий справиться с этой задачей, демонстрируется следующим фрагментом:

struct t {

...

struct s *p; /* р указывает на s */

};

struct s {

... struct t *q; /* q указывает на t */

};

Вся программа удивительно мала - правда, она использует вспомогательные программы вроде getword , уже написанные нами. Главная программа читает слова с помощью getword и вставляет их в дерево посредством addtree .

#include