Брайан Керниган - Язык программирования Си. Издание 3-е, исправленное

Объявление структуры, не содержащей списка переменных, не резервирует памяти; оно просто описывает шаблон, или образец структуры. Однако если структура имеет тег, то этим тегом далее можно пользоваться при определении структурных объектов. Например, с помощью заданного выше описания структуры point строка

struct point pt;

определяет структурную переменную pt типа struct point . Структурную переменную при ее определении можно инициализировать, формируя список инициализаторов ее элементов в виде константных выражений:

struct point maxpt = {320, 200};

Инициализировать автоматические структуры можно также присваиванием или обращением к функции, возвращающей структуру соответствующего типа.

Доступ к отдельному элементу структуры осуществляется посредством конструкции вида:

имя-структуры . элемент

Оператор доступа к элементу структуры .соединяет имя структуры и имя элемента. Чтобы напечатать, например, координаты точки pt , годится следующее обращение к printf :

printf("%d, %d", pt.x, pt.y);

Другой пример: чтобы вычислить расстояние от начала координат (0,0) до pt , можно написать

double dist, sqrt(double); dist = sqrt((double)pt.x * pt.x + (double)pt.y * pt.y);

Структуры могут быть вложены друг в друга. Одно из возможных представлений прямоугольника - это пара точек на углах одной из его диагоналей:

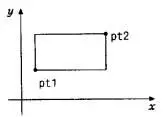
struct rect {struct point pt1; struct point pt2;};

Структура rect содержит две структуры point . Если мы объявим screen как

struct rect screen;

то

screen.pt1.x

обращается к координате x точки pt1 из screen .

Единственно возможные операции над структурами - это их копирование, присваивание, взятие адреса с помощью & и осуществление доступа к ее элементам. Копирование и присваивание также включают в себя передачу функциям аргументов и возврат ими значений. Структуры нельзя сравнивать. Инициализировать структуру можно списком константных значений ее элементов; автоматическую структуру также можно инициализировать присваиванием.

Чтобы лучше познакомиться со структурами, напишем несколько функций, манипулирующих точками и прямоугольниками. Возникает вопрос: а как передавать функциям названные объекты? Существует по крайней мере три подхода: передавать компоненты по отдельности, передавать всю структуру целиком и передавать указатель на структуру. Каждый подход имеет свои плюсы и минусы.

Первая функция, makepoint , получает два целых значения и возвращает структуру point .

/* makepoint: формирует точку по компонентам x и y */

struct point makepoint(int х, int у) {

struct point temp;

temp.x = х;

temp.у = у;

return temp;

}

Заметим: никакого конфликта между именем аргумента и именем элемента структуры не возникает; более того, сходство подчеркивает родство обозначаемых им объектов.

Теперь с помощью makepoint можно выполнять динамическую инициализацию любой структуры или формировать структурные аргументы для той или иной функции:

struct rect screen;

struct point middle;

struct point makepoint(int, int);

screen.pt1 = makepoint(0, 0);

screen.pt2 = makepoint(XMAX, YMAX);

middle = makepoint((screen.pt1.x + screen.pt2.x)/2, (screen.pt1.y + screen.pt2.y)/2);

Следующий шаг состоит в определении ряда функций, реализующих различные операции над точками. В качестве примера рассмотрим следующую функцию:

/* addpoint: сложение двух точек */

struct point addpoint(struct point p1, struct point p2)

{

p1.x += p2.x;

p1.y += p2.y;

return p1;

}

Здесь оба аргумента и возвращаемое значение - структуры. Мы увеличиваем компоненты прямо в р1 и не используем для этого временной переменной, чтобы подчеркнуть, что структурные параметры передаются по значению так же, как и любые другие.

В качестве другого примера приведем функцию ptinrect , которая проверяет: находится ли точка внутри прямоугольника, относительно которого мы принимаем соглашение, что в него входят его левая и нижняя стороны, но не входят верхняя и правая.

/* ptinrect: возвращает 1, если p в r, и 0 в противном случае */

int ptinrect(struct point р, struct rect r) {

return p.x >= r.pt1.x && p.x < r.pt2.x && p.y >= r.pt1.y && p.y < r.pt2.y;

}

Здесь предполагается, что прямоугольник представлен в стандартном виде, т.е. координаты точки pt1 меньше соответствующих координат точки pt2 . Следующая функция гарантирует получение прямоугольника в каноническом виде.