Ibrahim Dogan - Advanced PIC Microcontroller Projects in C

return z;

}

/* Define a function to subtract two complex numbers and return the result as

a complex number */

complex Subtract(complex i, complex j) {

complex z;

z.real = i.real - j.real;

z.imag = i.imag - j.imag;

return z;

}

/* Main program */

void main() {

complex a, b, c, d;

a.real = 2.0; a.imag =−3.0; // First complex number

b.real = 2.5; b.imag = 2.0; // second complex number

c = Add(a, b); // Add numbers

d = Subtract(a, b); // Subtract numbers

}

Figure 4.30: Program for Example 4.19

Two other complex numbers, c and d, are also declared, and the following complex number operations are performed:

The program calculates, c = a + b and, d = a – b

A projectile is fired at an angle of y degrees at an initial velocity of v meters per second. The distance traveled by the projectile (d), the flight time (t), and the maximum height reached (h) are given by the following formulas:

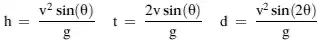
Write functions to calculate the height, flight time, and distance traveled. Assuming that g=9.81m/s², v=12 m/s, and θ=45°, call the functions to calculate the three variables. Figure 4.31 shows the projectile pattern.

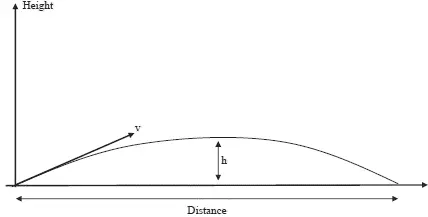
Figure 4.31: Projectile pattern

The required program is given in Figure 4.32 (program PROJECTILE.C). Three functions are defined: Height calculates the maximum height of the projectile, Flight_time calculates the flight time, and Distance calculates the distance traveled. In addition, a function called Radians converts degrees into radians to use in the trigonometric function sine . The height, distance traveled, and flight time are calculated and stored in floating point variables h, d, and t respectively.

/**********************************************************************

PROJECTILE CALCULATION

========================

This program calculates the maximum height, distance traveled, and the flight

time of a projectile. Theta is the firing angle, and v is the initial

velocity of the projectile respectively.

Programmer: Dogan Ibrahim

File: PROJECTILE.C

Date: May, 2007

***********************************************************************/

#define gravity 9.81

/* This function converts degrees to radians */

float Radians(float y) {

float rad;

rad = y * 3.14159 / 180.0;

return rad;

}

/* Flight time of the projectile */

float Flight_time(float theta, float v) {

float t, rad;

rad = Radians(theta);

t = (2.0*v*sin(rad)) / gravity;

return t;

}

float Height(float theta, float v) {

float h, rad;

rad = Radians(theta);

h = (v*v*sin(rad)) / gravity;

return h;

}

float Distance(float theta, float v) {

float d, rad;

rad = radians(theta);

d = (v*v*sin(2*rad)) / gravity;

return d;

}

/* Main program */

void main() {

float theta, v, h, d, t;

theta = 45.0;

v = 12.0;

h = Height(theta, v);

d = Distance(theta, v);

t = Flight_time(theta, v);

}

Figure 4.32: Program for Example 4.20

This chapter has discussed the important topics of functions and libraries. Functions are useful when part of a code must be repeated several times from different points of a program. They also make programs more readable and easier to manage and maintain. A large program can be split into many functions that are tested independently and, once all of them are working, are combined to produce the final program.

The mikroC language library functions have also been described briefly, along with examples of how to use several of these functions in main programs. Library functions simplify programmers’ tasks by providing ready and tested routines that can be called and used in their programs.

1. Write a function to calculate the circumference of a rectangle. The function should receive the two sides of the rectangle as floating point numbers and return the circumference as a floating point number.

2. Write a main program to use the function you developed in Exercise 1. Find the circumference of a rectangle whose sides are 2.3cm and 5.6cm. Store the result in a floating point number called MyResult.

3. Write a function to convert inches to centimeters. The function should receive inches as a floating point number and then calculate the equivalent centimeters.

4. Write a main program to use the function you developed in Exercise 3. Convert 12.5 inches into centimeters and store the result as a floating point number.

5. An LED is connected to port pin RB0 of a PIC18F452-type microcontroller through a current limiting resistor in current sinking mode. Write a program to flash the LED in five-second intervals.

6. Eight LEDs are connected to PORTB of a PIC18F452-type microcontroller. Write a program so that the LEDs count up in binary sequence with a one-second delay between outputs.

7. An LED is connected to port pin RB7 of a PIC18F452 microcontroller. Write a program to flash the LED such that the ON time is five seconds, and the OFF time is three seconds.

8. A text-based LCD is connected to a PIC18F452-type microcontroller in 4-bit data mode. Write a program that will display a count from 0 to 255 on the LCD with a one-second interval between counts.

9. A text-based LCD is connected to a PIC microcontroller as in Exercise 8. Write a program to display the text “Exercise 9” on the first row of the LCD.

10. Repeat Exercise 9 but display the message on the first row, starting from column 3 of the LCD.

11. A two-row text-based LCD is connected to a PIC18F452-type microcontroller in 4-bit-data mode. Write a program to display the text “COUNTS:” on row 1 and then to count repeatedly from 1 to 100 on row 2 with two-second intervals.

12. Write a program to calculate the trigonometric cosine of angles from 0 to 45 in steps of 1 and store the results in a floating point array.

13. Write a function to calculate and return the length of the hypotenuse of a right-angle triangle, given its two sides. Show how you can use the function in a main program to calculate the hypotenuse of a right-angle triangle whose two sides are 4.0cm and 5.0cm.

14. Write a program to configure port pin RB2 of a PIC18F452 microcontroller as the RS232 serial output port. Send character “X” to this port at 4800 baud.