Номер k любого хода может быть единственным способом представлен в виде
k = (2 r + 1)2 р -1.
Перемещаемый на этом ходе диск есть диск с номером p , и это — его ( r + 1)-е перемещение. Так как он начинает движение со стержня 0 и перемещается в направлении s p (1, если р нечетно, и 2 в противном случае), то на этом ходе диск перемещается с rs p -го на ( r + 1) s р -й стержень, где эти числа берутся по модулю 3.
Игра 34.
Попытаемся охарактеризовать значение р , дающее игре оптимум для данного n . Нам известно, что f 3( n − p )= 2 n - p − 1.
Должно выполняться
2 f 4( p − 1) + 2 n - p +1− 1 ≥ 2 f 4( р ) + 2 n - p − 1,
2 f 4( p + 1) + 2 n - p- 1− 1 ≥ 2 f 4( р ) + 2 n - p − 1.
Удобно пользоваться первыми разностями для функции f 4:
d ( р ) = f 4( p + 1) − f 4( p ).
Два приведенных выше соотношения могут быть переписаны следующим образом:
d ( p − 1) < 2 n - p -1, d ( р ) ≥ 2 n - p- 2.
Интересно рассматривать даже не d ( р ), а скорее 2 pd ( р ) = g ( р ):
g ( р − 1) ~ 2 n -2≤ g ( р ).
Можно еще упростить запись, беря не g ( р ), а величину
h ( р ) = log 2( g ( р )) = р + Iog 2( d ( р )).
Тогда получаем
h ( р − 1) < n − 1 ≤ h ( р ).
При данном n величина р — наименьшее целое, для которого h больше или равно n − 2.
Приведем здесь первые из полученных таким образом значений:
| n |
q |
f 4 |
p |
d |
h |
| 0 |
0 |
0 |
|
1 |
0 |
| 1 |
1 |
1 |
|
2 |
2 |
| 2 |
|
3 |
|
2 |
3 |
| 3 |
2 |
5 |
1 |
4 |
5 |
| 4 |
|
9 |
1 |
4 |
6 |
| 5 |
|
13 |
1 |
4 |
7 |
| 6 |
3 |
17 |
3 |
8 |
9 |
| 7 |
|
25 |
3 |
8 |
10 |
| 8 |
|
33 |
4 |
8 |
11 |
| 9 |
|
41 |
5 |
8 |
12 |
| 10 |
4 |
49 |
6 |
16 |
14 |
| 11 |
|
65 |
6 |
16 |
15 |
Мы добавили в таблицу переменное q , связанное с «треугольными» числами. Для n = q ( q + 1)/2 действительно убеждаемся, что
h ( р ) = h ( р − 1) + 2
в то время как для других n
h ( p ) = h ( p − 1) + 1.
Исходя из n , можно вычислить q :
q = целая_часть (( 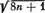 − 1)/2).
− 1)/2).
Имеем
h ( n ) = n + целая_часть (( 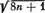 − 1)/2).
− 1)/2).
Покажите это по индукции. Исходя отсюда, вычисляется все. Таким образом, если n дано, то р — наименьшее целое, большее или равное
(2 n − 1 − 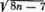 )/2.
)/2.
Игра 35.
Возьмем, например, игру с 50 дисками. Она реализуется переносом сначала 40 дисков на запасной стержень, а затем 10 последних дисков со стержня 0 на стержень 1, с использованием при этом только трех свободных стержней. Наконец, остается перенести начальные 40 самых маленьких дисков с запасного стержня на первый стержень, используя все 4 стержня.
Чтобы переместить 40 дисков с 4 стержнями, сводим задачу к перемещению 31 диска с 4 стержнями, а затем 9 с 3 стержнями…
Таким образом, дело сводится к разбиению 50 дисков на 8 сегментов:

Каждый сегмент перемещается с использованием 3 стержней, в чем мы следуем итеративной стратегии, которая уже описана выше. Единственный вопрос — это правильный выбор запасных стержней.
Договоримся работать с тремя стержнями 0, 1, 2, так что стержень 3 остается пустым и служит запасным стержнем при любом перемещении какого-либо сегмента. Более точно, перемещение сегмента р со стержня d на стержень а осуществляется с помощью изученной выше процедуры Н , в которой запасным стержнем является стержень 3.
Сегмент 1 перемещается в каждый из двух ходов подряд (под ходом я понимаю последовательность операций, реализующих процедуру Н ), всегда в одном и том же направлении.
Мы сохраняем предыдущую итеративную стратегию, но понимаем ее как стратегию для сегментов. На компьютере это может пройти очень быстро. Вполне вероятно, что робот может осуществить одно перемещение за несколько секунд. Тогда на всю игру потребуется не более чем несколько часов…
Читать дальше

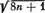 − 1)/2).
− 1)/2).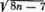 )/2.
)/2.











