Жак Арсак - Программирование игр и головоломок

Головоломка 7.

Возьмем n = 3 n ' + 2. Тогда (2 n − 1)/3 = 2 n ' + 1.

По общему правилу, непосредственно следующий за нечетным числом 2 n ' + 1 элемент равен (3(2 n ' + 1) + 1)/2 = 3 n ' + 2.

Если n дает n ' при переходе ( p , q ), q > 1, т. е. если n имеет вид n = (2 p(2 q n ' + 1)/3 p ) − 1, то

n '' = ( n − 1)/2 = (2 p −1(2 qn ' + 1)/З p ) − 1.

Как и следовало ожидать, это имеет в точности тот смысл, что если деление на З p можно выполнить нацело, то в связи с этим возникает соотношение между ( p , q ) и n '.

Если n " увеличить на 1, а затем умножить на 3 p −1/2 p −1, то получится (2 qn ' + 1)/3.

Тогда нужно уменьшить результат на 1: получим (2 qn ' − 2)/3. Но это число делится на 2, так что с помощью перехода ( p − 1, 1) число n " дает

(2 q −1 n ' − 1)/3.

По общим правилам получаем

3 ((2 q −1 n ' − 1)/3) + 1 = 2 q −1 n ',

а затем n', что и доказывает наше утверждение.

Если вы примените это правило перехода к 4 k + 1, то нужно добавить 1, что дает 4 k + 2, делящееся на 2, но не на 4. Делим на 2 и умножаем на 3, что дает 6 k + 3. Уменьшаем на 1 и затем делим на 2, и получается З k + 1.

Если k нечетно, то это — элемент, следующий за k ; так что за числом вида 4 k + 1 с k нечетным следуют те же величины, что и за k .

Если k четно, то 4 k + 1 дает 3 k + 1.

Если существует цикл с единственным переходом p , q , т. е.

n = (2 p (2 qn + 1)/3 p ) − 1,

то это возможно только в случае, когда существует такая пара p , q , что число

(З p − 2 p )/(2 p + q − З p )

— целое. Мы показали, что такой пары ( p , q ) нет.

Головоломка 10.

9*АВСДЕ + АВСДЕ = 10*АВСДЕ, что можно записать как АВСДЕ0. Отсюда получаем зашифрованное сложение:

FGHIJ + ABCDE = ABCDE0

Это показывает, что A = 1. Далее, J + E не может быть нулем, следовательно, J + Е = 10 и для I есть кое-что «в уме». Сумма F + A дает AB с A = 1, так что сумма F + 1, к которой, может быть, добавлено что-то «в уме», должна дать число, большее 9. Это может быть только в случаях 1 + 8 + 1 = 10, 9 + 1=10 или 1 + 9 + 1 = 11. Но, так как B ≠ A , то B = 0.

Тогда в сумме G + B рассмотрим цифру C как цифру единиц. Так как В = 0, то это означает, что для G «в уме» кое-что есть (потому что G ≠ С ).

Отсюда получаем схему операции сложения:

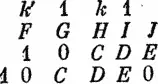
Запишем, что A + B + C + D + E + F + G + H + I + J = 45,

А = 1, B = 0.

Запишем пять операций сложения с учетом переносов в старший разряд:

J + E = 10,

1 + I + D = 10 k + E ,

k + H + C = 10 + D ,

1 + G + В = 10 k ' + С ,

k ' + F + A = 10.

Сложим их все. Вам остается

C + D + E = 17 − 9( k + k ').

Но С + D + E не может быть меньше, чем 2 + 3 + 4 = 9, и не может быть больше, чем 6 + 7 + 9 (если F = 8 и k ' = 1). Не может быть, чтобы у вас одновременно выполнялись соотношения k = k ' = 1 (что давало бы отрицательную сумму С + D + E ). Но не может быть и равенства k + k ' = 1, так как тогда было бы С + D + E = 17 − 9 = 8, что слишком мало. Следовательно, k = k ' = 0. Составим окончательную систему

J + E = 10,

I + D + 1 = E ,

H + C = 10 + D ,

G + 1 = С ,

F = 9.

Закончите вы с помощью программы.

Головоломка 11.

Обозначим через a i цифры исходного числа, b i — цифры результата, k i — цифры «в уме»:

3 a i + k i = b i + 10 k i +1.

Сумма всех a i равна 45, как и сумма всех b i . Обозначим через K сумму всех k i :

3*45 + K = 45 + 10* K дает К = 10.

Мы знаем, что дает «в уме» каждая цифра:

1 дает 0, 2 дает 0, 3 дает 0 или 1 в зависимости от того, что хранится «в уме» над 3.

4 дает 1, 5 дает 1, 6 дает 1, потому что не может случиться 3*6 + 2, что давало бы «в уме» 2, но цифру единиц 0;

7, 8 и 9 дают 2.

Для того, чтобы сумма величин «в уме» была равна 10, нужно, чтобы 3 давало 1 «в уме». Так как 3*3 + 1 (с цифрой единиц, равной 0) случиться не может, то нужно, чтобы «в уме» над 3 было 2. Следовательно, 3 стоит слева от 7, 8 или 9. В частности, 3 не может стоять на правом конце.

Остальное просто, если вы будете следовать методу, указанному в разделе «Условия». Вот таблица: