Жак Арсак - Программирование игр и головоломок

Если вы находите это совершенно элементарным, вы можете изучить, являются ли данные цепочки обращениями друг друга с точностью до пробелов. Вы можете также увидеть, является ли цепочка палиндромом (т. е. совпадает со своим обращением) с точностью до пробелов, Так, палиндромами являются

А РОЗА УПАЛА НА ЛАПУ АЗОРА

АРГЕНТИНА МАНИТ НЕГРА

Попытайтесь получить правильную (это уж как минимум) и элегантную программу.

Головоломка 31.Анаграмма.

Еще одна головоломка, вопреки ее внешнему виду, Дело в том, чтобы сказать, являются ли две цепочки букв анаграммами друг друга (т. е. получаются ли они друг из друга перестановками букв). Эта задача имеет совершенно различный вид в зависимости от того, разрешите ли вы себе изменять обе цепочки или порождать новые цепочки, или нет. Выбор я предоставляю вам… Может быть, вы заметите, что различные решения следует оценивать в зависимости от соотношения между размерами цепочек и используемого алфавита. Подумайте о крайних случаях: алфавит из 26 букв и цепочка из 1000 символов; алфавит из 1000 символов (это вроде китайского…) и цепочка из 10 символов.

Головоломка 32.Анаграмма с точностью до пробелов.

Та же головоломка, но, кроме того, пробелы не считаются. Вы можете ее еще немного обобщить: являются ли две страницы текста анаграммами одна другой, не считая знаков препинания?

??* Головоломка 33.Переставить две части вектора.

Вам дана таблица a с n элементами. Требуется переставить части с номерами от 1 до m и от m + 1 до n (рис. 33).

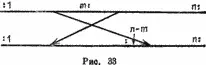
Порядок элементов в каждой ив частой должен быть сохранен [17] Вот другая и, на мой взгляд, более правильная формулировка этой задачи: циклически сдвинуть элементы n -вектора на m позиций влево. — Примеч. ред. . Вы не должны использовать вспомогательную таблицу, Каждый элемент должен быть перемещен не более одного раза.

Это — довольно любопытная задача, которая была предложена мне Давидом Грисом, и которую он исследовал в своей книге [GRI] Это — один из редких случаев, когда я не смог вывести программу из гипотезы рекуррентности, как я это обычно делал [ARS]. В данном случае я сначала придумал программу (ничего особенного, вы ее, конечно, прекрасно составите). И только после того — именно после того — я смог показать, почему эта программа работает правильно.

* Головоломка 34.Задача о равнинах.

Вам дается упорядоченная таблица каких-то элементов, например, телефонный справочник (где фамилии расположены в алфавитном порядке. Здесь мы не учитываем имен). В таблице могут встретиться омонимы (иначе говоря, последовательности из совпадающих элементов), как в телефонном справочнике. Требуется найти наиболее длинные омонимы: больше ли МАРТЫНОВых, чем СЕМЕНОВых?

Я использовал для этой головоломки название, данное ей в книге Давида Гриса [GRI]. Если вместо того, чтобы веять для иллюстрации таблицу фамилий, вы берете

таблицу чисел, расположенных в неубывающем порядке, то такая таблица составлена иэ участков возрастания, подъемов и ровных участков, «равнин». Тогда нужно найти наиболее длинную равнину.

Эта задача оказывается не вполне одной и той же в зависимости от того, ищете ли вы только наибольшую длину равнины (что делает Д. Грис) или ищете одновременно и длину ряда омонимов и сам наиболее часто встречающийся омоним (что предлагаю вам я).

G этой задачей связана неприятная для меня история. Я намеревался продумать эту задачу в Нанси также, впрочем, как и Давид Грис. Я довольно легко обнаружил два решения, различные по духу, но не по виду, что поставило передо мной задачи преобразования программ (каким образом различные отправные точки могут привести, с точностью до нескольких манипуляций, к одной и той же программе). Как и рассказывает в своей книге Давид Грис, я очень гордился своими решениями, пока не обнаружил в той же книге Д. Гриса решение, принадлежащее Майклу Гриффиту: его решение намного проще…

Сумеете ли вы найти простое решение?

??** Головоломка 35.Самая длинная возрастающая подпоследовательность.

Пусть дана таблица a из n каких-либо чисел (но если это может доставить вам удовольствие — из натуральных чисел. Это неважно). Подпоследовательность этой таблицы есть последовательность чисел, выделенная в порядке возрастания номеров. Более точно, последовательность