Здесь речь идет совсем о другом. Эта задача была предложена как одна из четырех тем на конкурсе программирования в АФСЕТ несколько лет назад. Вам дана прямоугольная решетка для кроссворда. Найдите белый (т. е. не содержащий вычеркнутых черных клеток) прямоугольник наибольшей площади, вписанный в решетку (квадрат есть частный случай прямоугольника).
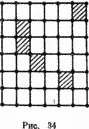
На рис. 34 есть прямоугольник площади 8 в левом нижнем углу и есть квадрат площади 9. Это — хороший ответ. Программа, которую вы должны составить, должна читать размеры сетки (число строк и столбцов), затем— координаты черных полей и, наконец, давать прямоугольник наибольшей площади, например, указанием координат двух противоположных вершин.
Для программистов на конкурсе АФСЕТ это не было легкой задачей. Она оказалась едва ли не наиболее трудной задачей, будучи единственной задачей, доставившей мне затруднения (см. головоломку 22, другое упражнение на том же конкурсе). Один из соревнующихся достиг цели, решительно пренебрегая эффективностью. Вы-то не очень ограничены временем (по крайней мере временем размышления или временем программирования). Попытайтесь составить программу, время вычисления которой не слишком быстро растет вместе с размером сетки.
Головоломка 38.Математическая композиция.
Ж.-К. Байиф [BAI], французский язык которого очень отточен, представил эту головоломку под названием «арифметическая композиция» в своей книге, из которой в ее и заимствую, Композиция состоит из четырех вопросов, связанных с вычислением площади. Один из вопросов относится к полной поверхности куба, сторона которого измеряется целым числом метров, Вот ответы учеников на различные вопросы:
| Альбер |
8 |
16 |
12 |
16 |
| Бернар |
12 |
16 |
12 |
18 |
| Клод |
12 |
18 |
12 |
18 |
| Дени |
16 |
18 |
12 |
20 |
| Эрнест |
8 |
16 |
10 |
16 |
| Фернан |
12 |
12 |
12 |
22 |
| Гюстав |
16 |
18 |
12 |
20 |
| Анри |
8 |
16 |
10 |
16 |
| Исидор |
16 |
12 |
12 |
20 |
| Жюль |
20 |
12 |
12 |
20 |
(Это — величины площадей в квадратных метрах, предложенные учениками.) Преподаватель ставит 5 за верный ответ и 0 за неверный ответ. Один-единственный из учеников получил 0. Кто оказался первым? Вне всякого сомнения, вы можете сказать больше. Эта головоломка кажется мне особенно подходящей для ее решения на компьютере…
?? Головоломка 39.Другая головоломка Давида Гриса.
Пусть дан вектор, образованный n целыми числами. Подпоследовательностью этого вектора называется набор элементов, в котором индексы идут подряд. Найти подпоследовательность с максимальной суммой. Если вы предпочитаете другую формулировку, то найдите индексы i , j , для которых величина
a i + a i +1+ … + a j −1+ a j
максимальна. Внимание: время вычисления не должно расти намного быстрее, чем n , когда n увеличивается…
Эта головоломка до некоторой степени напоминает головоломку о возрастающих подпоследовательностях, но она гораздо менее сложна. Подумайте: линейная зависимость от n ! Да ведь это, грубо говоря, означает, что каждый элемент вектора рассматривается только один раз. Вам следует составить цикл
ДЛЯ i := 1 ШАГ 1 ДО n ВЫПОЛНЯТЬ … ВЕРНУТЬСЯ
И никаких циклов в этом цикле! В ответе вы получаете искомые индексы. Озадачивающе, не так ли? Я потерял на это немало времени. И тем не менее, какое простое решение!
Как вы находите?
У вас возникли затруднения, — вы не знаете, как приступить к игре или головоломке. Я не хочу предлагать вам готовое решение, иначе в чем будет удовольствие? Но, вероятно, нижеследующие указания наведут вас на правильный путь. Если бы я мог использовать дискетку вместо книги, я разложил бы эти указания на как можно большее число уровней, чтобы вы были в состоянии брать из них тот строгий минимум, который позволит вам продолжать решение. Но и в книге вы всегда можете прочесть только начало и — как только искра вспыхнет — отложить книгу и завершить решение самостоятельно.
Некоторые упражнения кажутся мне настолько очевидными, что я ничего про них не скажу. Но, конечно, это субъективная точка зрения: они могут не казаться очевидными вам. Может быть, потому, что вы не видите, в чем задача: разберите простые случаи вручную, В любом случае старайтесь сформулировать задачу с максимальной возможной полнотой, Если и после этого вы по- прежнему не видите, как вам ее охватить, поговорите с друзьями или с приятелями, Я умышленно не собираюсь сообщать вам все. Эта книга написана для того, чтобы вы стали программировать. Вам играть…
Читать дальше













