Жак Арсак - Программирование игр и головоломок

Не поступайте так. Эта задача при всем том нетрудная… Рис. 29 дает пример цепи.

* Головоломка 23.Последовательность 0—1—4—6.

Это головоломка, на которую я натолкнулся, работая над своей диссертацией на ученую степень по физике. Я занимался сетями антенн для радиоастрономии. Сеть антенн состоит из основания, на котором по одной линии размещены отдельные антенны, доставляющие информацию о наблюдаемых нами звездах. Каждая нара антенн дает информацию о некоторой величине, пропорциональной расстоянию между двумя антеннами этой пары. Нас интересуют значения этой величины, образующие арифметическую прогрессию. Таким образом, нужно было располагать антенны таким образом, чтобы расстояния между равными парами образовывали арифметическую прогрессию. Я предложил систему из 4 антенн, расположенных на прямой в точках с абсциссами 0 1 4 6.

Тогда получаемые из них 6 различных пар приводят к расстояниям между антеннами, пропорциональным следующим числам:

0—1 1

4—6 2

1—4 3

0—4 4

1—6 5

0—6 6

Можно сформулировать задачу по-другому. Нужно найти последовательность натуральных чисел a 1, a 2, …, a n — последовательность, которую можно предполагать возрастающей — такую, чтобы попарные разности членов этой последовательности a j − a i ( j > i ) были попарно различны и образовывали последовательность всех целых чисел от 1 до n ( n − 1)/2.

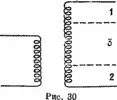
Это — еще и проблема трансформатора (см. рис. 30), Если включить во вторичную обмотку 4 выхода так, чтобы число витков между первым и другими выходами находилось в отношениях 1, 4 и 6, то можно получить 6 напряжений на выходе, образующих арифметическую прогрессию.

Опустим другие физические задачи, порождающие такие последовательности. Четырехчленная последовательность 0—1—4—6, по-видимому, является наибольшей последовательностью, обладающей свойством порождать последовательность первых целых чисел, не пропуская и не повторяя дважды ни одного из них, при попарном вычитании членов этой последовательности.

Так, для 5 целых можно образовать 10 разностей. Поэтому крайние члены должны быть a 1= 0, a 5= 10. Чтобы получить в виде разности 9 из двух членов последовательности, нужно, чтобы либо было a 2= 1, и тогда a 5− a 2= 9, либо a 4= 9. Эти два решения легко получаются одно из другого операцией симметрии, Поэтому положим a 2= 1.

К этому моменту мы получили уже a 1= 0, a 2= 1, a 5= 10. Чтобы получить разность, равную 8, нужно взять

— либо a 3= 2, но тогда разность, равная 1, получается дважды:

a 3− a 2= a 2− a 1

— либо a 4= 8,

— либо a 4= 9, но тогда снова дублируется разность 1. Следовательно, a 1= 0, a 2= 1, a 4= 8, a 5= 10.

Достаточно теперь пересмотреть одно за другим возможные значения а 3и удостовериться, что каждое ив них дублирует какую-то разность.

Для a 3, равного 2, дублируется разность 1:

3 2

4 4

5 5

6 2

7 1

Таким образом, нет последовательности из 5 целых, попарные разности которых порождают 10 первых натуральных чисел. Допустим теперь возможность повторений в последовательности разностей. Можно ли с помощью 5 членов породить — с помощью их разностей — 9 первых натуральных чисел?

Об этих последовательностях ничего не известно. Пусть дано число n членов последовательности; каково наибольшее число последовательных целых чисел, начиная с 1, которые можно получить с помощью попарных разностей членов последовательности?

Запрограммировать это не очень трудно. Но берегитесь чересчур долгих вычислений!

?** Головоломка 24.Прогулка королевы.

Нет, не в Булонском лесу, если говорить серьезно… Прогулки фигур на шахматной доске — классический сюжет для головоломок. Эйлеровский конь должен обойти всю шахматную доску и вернуться на поле, с которого отправился в путь, не попадая дважды ни на одну клетку. Это настолько общеизвестно, что это уже и не головоломка. Но если вы не знаете решения, я не мешаю вам попробовать.

Случай «королевы» (ферзя) — немного другой. Эта фигура может перемещаться по горизонтали, по вертикали или по диагонали. Назовем «движением» перемещение на некоторое число полей в определенном направлении, Разрешается много раз проходить по одному и тому же полю. Но требуете пройти все поля эа наименьшее возможное число движений, причем, конечно, нужно вернуться на исходное поле. Так как число движений не дано, то не попытаетесь ли вы сначала проделать все вручную, чтобы угнать верхнюю границу…