Иван Братко - Программирование на языке Пролог для искусственного интеллекта

К сожалению, если X — это внутренняя вершина, то такой способ не работает, поскольку возникает проблема, иллюстрацией к которой служит рис. 9.11. Вершина X имеет два поддерева Леви Прав. После удаления вершины X в дереве образуется "дыра", и поддеревья Леви Правтеряют свою связь с остальной частью дерева. К вершине А оба эти поддерева присоединить невозможно, так как вершина А способна принять только одно из них.

Если одно из поддеревьев Леви Правпусто, то существует простое решение: подсоединить к А непустое поддерево. Если же оба поддерева непусты, то можно использовать следующую идею (рис. 9.12): если самую левую вершину Y поддерева Правпереместить из ее текущего положения вверх и заполнить ею пробел, оставшийся после X, то упорядоченность дерева не нарушится. Разумеется, та же идея сработает и в симметричном случае, когда перемещается самая правая вершина поддерева Лев.

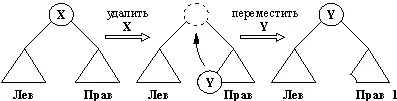
Рис. 9. 2. Заполнение пустого места после удаления X.

На рис. 9.13 показана программа, реализующая операцию удаления элементов в соответствии с изложенными выше соображениями. Основную работу по перемещению самой левой вершины выполняет отношение

удмин( Дер, Y, Дер1)

Здесь Y — минимальная (т.е. самая левая) вершина дерева Дер, а Дер1 — то, во что превращается дерево Дерпосле удаления вершины Y.

Существует другой, элегантный способ реализация операции добавить и удалить . Отношение добавить можно сделать недетерминированным в том смысле, что новый элемент вводится на произвольный уровень дерева, а не только на уровень листьев. Правила таковы:

Для того, чтобы добавить X в двоичный справочник Д, необходимо одно из двух:

• добавить X на место корня дерева (так, что X станет новым корнем) или

• если корень больше, чем X, то внести X в левое поддерево, иначе — в правое поддерево.

уд( дер( nil, X, Прав), X, Прав).

уд( дер( Лев, X, nil), X, Лев).

уд( дер( Лев, X, Прав), X, дер( Лев,Y, Прав1) ) :-

удмин( Прав, Y, Прав1).

уд( дер( Лев, Кор, Прав), X, дер( Лев1, Кор, Прав) ) :-

больше( Кор, X),

уд( Лев, X, Лев1).

уд( дер( Лев, Кор, Прав), X, дер( Лев, Кор, Прав1) ) :-

больше( X, Кор),

уд( Прав, X, Прав1).

удмин( дер( nil, Y, Прав), Y, Прав).

удмин( дер( Лев, Кор, Прав), Y, дер( Лев1, Кор, Прав) ) :-

удмин( Лев, Y, Лев1).

Рис. 9.13.Удаление элемента из двоичного справочника.

Трудным моментом здесь является введение X на место корня. Сформулируем эту операций в виде отношения

добкор( Д, X, X1)

где X — новый элемент, вставляемый вместо корня в Д, а Д1 — новый справочник с корнем X. На рис. 9.14 показано, как соотносятся X, Д и Д1. Остается вопрос: что из себя представляют поддеревья L1 и L2 (или, соответственно, R1 и R2) на рис. 9.14?

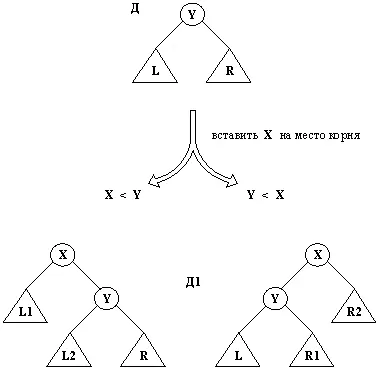
Рис. 9.14. Внесение X в двоичный справочник в качестве корня.

Ответ мы получим, если учтем следующие ограничения на L1, L2:

• L1 и L2 — двоичные справочники;

• множество всех вершин, содержащихся как в L1, так и в L2, совпадает с множеством вершин справочника L;

• все вершины из L1 меньше, чем X; все вершены из L2 больше, чем X.

Отношение, которое способно наложить все эти ограничения на L1, L2, — это как раз и есть наше отношение добкор. Действительно, если бы мы вводили X в L на место корня, то поддеревьями результирующего дерева как раз и оказались бы L1 и L2. В терминах Пролога L1 и L2 должны быть такими, чтобы достигалась цель

добкор( L, X, дер( L1, X, L2) ).

Те же самые ограничения применимы к R1, R2:

добкор( R, X, дер( R1, X, R2) ).

На рис. 9.15 показана программа для "недетерминированного" добавления элемента в двоичный справочник.

добавить( Д, X, Д1) :- % Добавить X на место корня

добкор( Д, X, Д1).

добавить( дер( L, Y, R), X, дер( L1, Y, R) ) :-

больше( Y, X), % Ввести X в левое поддерево

добавить( L, X, L1).

добавить( дер( L, Y, R), X, дер( L, Y, R1) ) :-

больше( X, Y), % Ввести X в правое поддерево

добавить( R, X, R1).

добкор( nil, X, дер( nil, X, nil) ). % Ввести X в пустое дерево

добкор( дер( L, Y, R), X, дер( L1, X, дер( L2, Y, R) )) :-

больше( Y, X),

добкор( L, X, дер( L1, X, L2) ).