Александр Леоненков - Самоучитель UML

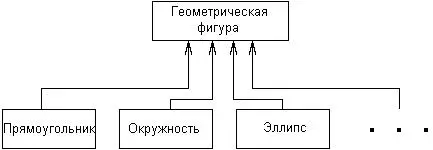
Рис. 5.13.Пример графического изображения отношения обобщения классов

С целью упрощения обозначений на диаграмме классов совокупность линий, обозначающих одно и то же отношение обобщения, может быть объединена в одну линию. В этом случае данные отдельные линии изображаются сходящимися к единственной .стрелке, имеющей с ними общую точку пересечения (рис. 5.14).

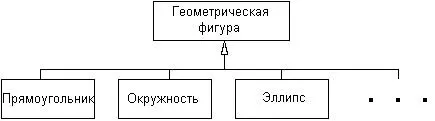
Рис. 5.14.Вариант графического изображения отношения обобщения классов для случая объединения отдельных линий

Это обозначение по форме соответствует графу специального вида, который рассматривался в главе 2, а именно – иерархическому дереву. В этом случае класс-предок является корнем этого дерева, а классы-потомки – его листьями. Отличие заключается в возможности указания на диаграмме классов потенциальной возможности наличия других классов-потомков, которые не включены в обозначения представленных на диаграмме классов (многоточие вместо прямоугольника).

Рядом со стрелкой обобщения может размещаться строка текста, указывающая на некоторые дополнительные свойства этого отношения. Данный текст будет относиться ко всем линиям обобщения, которые идут к классам-потомкам. Другими словами, отмеченное свойство касается всех подклассов данного отношения. При этом текст следует рассматривать как ограничение, и тогда он записывается в фигурных скобках.

В качестве ограничений могут быть использованы следующие ключевые слова языка UML:

• {complete} – означает, что в данном отношении обобщения специфицированы все классы-потомки, и других классов-потомков у данного класса-предка быть не может. Пример – класс Клиент_банка является предком для двух классов: Физическое_лицо и Компания, и других классов-потомков он не имеет. На соответствующей диаграмме классов это можно указать явно, записав рядом с линией обобщения данную строку-ограничение;

• {disjoint} – означает, что классы-потомки не могут содержать объектов, одновременно являющихся экземплярами двух или более классов. В приведенном выше примере это условие также выполняется, поскольку предполагается, что никакое конкретное физическое лицо не может являться одновременно и конкретной компанией. В этом случае рядом с линией обобщения можно записать данную строку-ограничение;

• {incomplete} – означает случай, противоположный первому. А именно, предполагается, что на диаграмме указаны не все классы-потомки. В последующем возможно восполнить их перечень не изменяя уже построенную диаграмму. Пример – диаграмма класса «Автомобиль», для которой указание всех без исключения моделей автомобилей соизмеримо с созданием соответствующего каталога. С другой стороны, для отдельной задачи, такой как разработка системы продажи автомобилей конкретных моделей, в этом нет необходимости. Но указать неполноту структуры классов-потомков все же следует;

• {overlapping} – означает, что отдельные экземпляры классов-потомков могут принадлежать одновременно нескольким классам. Пример – класс «Многоугольник» является классом-предком для класса «Прямоугольник» и класса «Ромб». Однако существует отдельный класс «Квадрат», экземпляры которого одновременно являются объектами первых двух классов. Вполне естественно такую ситуацию указать явно с помощью данной строки-ограничения.

С учетом возможности использования строк-ограничений диаграмма классов (рис. 5.14) может быть изображена без многоточий и без потери информации (рис. 5.15).

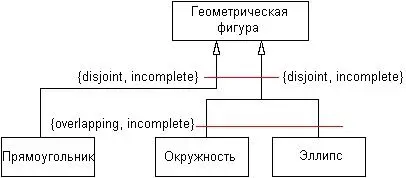
Рис. 5.15.Вариант графического изображения отношения обобщения классов с использованием строки-ограничения

Чтобы проиллюстрировать особенности использования отношения обобщения, преобразуем один из рассмотренных ранее примеров изображения классов в графическую нотацию языка UML. В качестве такого примера рассмотрим иерархию вложенности классов для абстрактного класса «Автомобиль» (см. рис. 1,2, 2.7). Как нетрудно заметить, отношение между отдельными классами на этих рисунках есть именно отношение обобщения, которое в языке UML имеет специальное графическое обозначение. С учетом этой графической нотации, фрагмент семантической сети для представления иерархии класса «Автомобиль» (см. рис. 2.7) может быть представлен в виде следующей диаграммы классов (рис. 5.16).