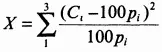Джулиан Бакнелл - Фундаментальные алгоритмы и структуры данных в Delphi

В таблице 6.1 для каждого возможного события приведена вероятность его возникновения и, кроме того, указано ожидаемое количество появлений каждого из событий для 100 бросков. (Ожидаемое количество появлений событий представляет собой просто результат умножения вероятности на общее количество событий.)

Одного взгляда достаточно, чтобы сказать, что две решки выпадают чаще, чем этого следует ожидать, однако достаточно ли велико отклонение, чтобы можно было сказать, что монеты имеют смещенный центр тяжести? Давайте посмотрим на разброс (т.е. отличие) полученных и ожидаемых результатов. Чтобы выделить разности и избавиться от отрицательных значений, возведем их в квадрат. Сумма полученных квадратов разностей и будет служить оценкой случайности результатов проведенных тестов. В нашем случае вычисление суммы квадратов разностей дает 26 (= 3(^2^) +1(^2^) + (-4)(^2^)). Но подождите-ка минутку, нам нужно каким-то образом учесть вероятность возникновения каждого события. Так для события "орел и решка" квадрат разности должен быть больше, чем для события "две решки", хотя бы только потому, что первое событие должно происходить чаще. Другими словами, разница 3 для события "две решки" будет намного более значительна, чем разница 1 для события "орел и решка". Поэтому давайте разделим каждый квадрат разности на ожидаемое количество появлений соответствующего события. Новая сумма будет вычисляться следующим образом:

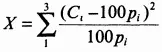
где С(_i_) - наблюдаемое количество, a p(_i_) - вероятность возникновения события i. Для наших данных значение X будет равно 1.02. Полученная нами сумма известна под названием критерия хи-квадрат (chi-squared value). Полученное значение можно найти в таблице стандартного распределения хи-квадрат (см. табл. 6.2).

Таблица 6.2. Процентные точки распределения хи-квадрат

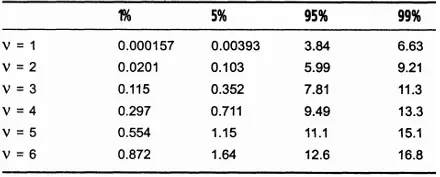
Вид таблицы слегка пугает, но понять ее совсем не сложно. Значения, приведенные в таблице, представляют собой значения распределения хи-квадрат для v степеней свободы (греческая буква v - это стандартный символ для обозначения степеней свободы). В свободной интерпретации можно сказать, что значение степеней свободы на единицу меньше количества возможных типов событий. В нашем случае возможны три типа событий: "две решки", "орел и решка" и "два орла". Следовательно, для нашего эксперимента количество степеней свободы будет равно 2. Строка для v = 2 содержит четыре значения - по одному значению в каждом из четырех столбцов. Значение в столбце 1% (0.0201) можно интерпретировать следующим образом: "Значение критерия X должно быть меньше 0.0201 только 1% времени". Другими словами, при повторении эксперимента 100 раз только примерно в одном из них будет получено значение X, меньшее 0.0201. Если будет обнаружено, что во многих экспериментах будет получено значение меньше 0.0201, можно будет с достаточно высокой степенью уверенности сказать, что бросание монет не является случайным событием, т.е. монеты имеют смещенный центр тяжести. То же самое можно сказать и для столбца 5%. О столбце 95% можно сказать, что значение параметра X должно быть меньше 5.99 примерно 95% времени или, что эквивалентно, значение параметра X должно быть больше 5.99 примерно 5% времени. Аналогичные рассуждения справедливы и для столбца 99%.

Полученное нами значение параметра X попадает в диапазон от 5% до 95%, т.е. на его основе мы не можем прийти к четкому заключению о смещенном центре тяжести монет. Приходится предполагать, что монеты являются настоящими (без всяких "хитростей"). Если же, с другой стороны, значение X было равно 10, можно было бы сказать, что такая ситуация может складываться не более чем в 1% экспериментов (10 больше чем 9.21 - значения для столбца 99%). Это послужило бы веским доказательством того, что монеты имеют смещенный центр тяжести. Конечно, потребуется провести большее количество экспериментов, и посмотреть, каким образом получаемые данные соотносятся со стандартным распределением хи-квадрат. По такому расширенному набору данных можно будет более точно оценить случайность получаемых данных. Не хотелось бы делать выводы, основываясь на результатах, которые согласно теории вероятностей, хотя и редко, но все же могут быть получены.