Джулиан Бакнелл - Фундаментальные алгоритмы и структуры данных в Delphi

Листинг 12.25. Рекурсивное вычисление LCS

function TtdStringLCS.slGetCell(aFromInx, aToInx : integer): integer;

var

LCSData : PtdLCSData;

NorthLen: integer;

WestLen : integer;

begin

if (aFromInx = 0) or (aToInx = 0) then

Result := 0

else begin

LCSData := FMatrix[ aFromInx, aToInx];

if (LCSData <> nil) then

Result := LCSData^.ldLen else begin

{создать новый элемент}

New(LCSData);

{если два символа совпадают, необходимо увеличить значение счетчика относительно элемента, расположенного к северо-западу от данного, т.е. предшествующего элемента}

if (FFromStr[aFromInx] = FToStr [aToInx]) then begin

LCSData^.ldPrev := ldNorthWest;

LCSData^.ldLen := slGetCell(aFromInx-1, aToInx-1) + 1;

end

{в противном случае текущие символы различаются: необходимо использовать максимальный из элементов, расположенных к северу и западу (выбор элемента расположенного к западу предпочтительнее)}

else begin

NorthLen := slGetCell(aFromInx-1, aToInx);

WestLen := slGetCell(aFromInx, aToInx-1);

if (NorthLen > WestLen) then begin

LCSData^.ldPrev := ldNorth;

LCSData^.ldLen := NorthLen;

end

else begin

LCSData^.ldPrev := ldWest;

LCSData^.ldLen := WestLen;

end;

end;

{установить значение элемента матрицы}

FMatrix[aFromInx, aToInx] := LCSData;

{вернуть длину данной LCS}

Result := LCSData^.ldLen;

end;

end;

end;

Первое существенное различие состоит в том, что не нужно генерировать нулевые значения для ячеек, расположенных вдоль верхней и правой сторон матрицы. Теперь эту задачу выполняет простой оператор If. (Честно говоря, в итеративном варианте вычисления LCS можно было бы обойтись без вычисления этих значений, но в этом случае внутренний код цикла оказался бы значительно сложнее для понимания и поддержки. Поэтому для простоты мы заранее вычисляем значения этих ячеек.) Если значение ячейки уже вычислено, мы просто возвращаем ее длину LCS. Если нет, необходимо выполнить ту же проверку, что и в предыдущем случае: совпадают ли два символа? Если да, то необходимо добавить единицу к значению LCS ячейки, расположенной к северо-западу от данной. Если нет, необходимо использовать большее из значений длины LCS ячеек, расположенных к северу и к западу от текущей. Естественно, эти значения LCS вычисляются в результате рекурсивных вызовов этой подпрограммы.

Применив обе версии (итеративную и рекурсивную), я сгенерировал матрицу для вычисления LCS слов "illiteracy" и "innumeracy". (Длина LCS этих слов равна 6 и выглядит как "ieracy".) Результаты этих немалых трудов приведены в таблицах 12.2 и 12.3. При использовании рекурсивной версии многие ячейки вообще не вычисляются (они помечены знаком вопроса). Эти ячейки образуют часть заключительной LCS.

Таблица 12.2. Итеративная матрица LCS слов "illiteracy" и "innumeracy".

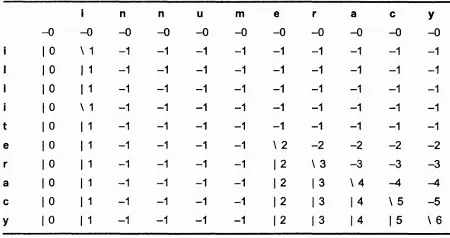
Таблица 12.3. Рекурсивная матрица LCS слов "illiteracy" и "innumeracy".

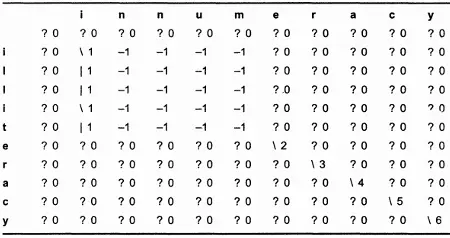
Итак, мы получили матрицу, которая определяет наиболее длинную общую подпоследовательность. Как ее можно использовать? Одна возможность связана с реализацией подпрограммы, которая создает текстовый файл, описывающий изменения, называемые последовательностью редактирования (edit sequence). Это может упростить создание аналогичной подпрограммы для текстового файла - что, собственно, является конечной целью данного раздела.

Код реализации простой технологии обхода, которая может быть приведена в соответствие с нашими потребностями, показан в листинге 12.26. Подпрограмма содержит два метода: первый вызывается пользователем с указанием имени файла, а второй представляет собой рекурсивную подпрограмму, которая записывает данные в файл. Весь основной объем работы выполняется во второй подпрограмме. Поскольку в матрице путь LCS кодируется в обратном направлении (т.е. для определения пути необходимо начать с конца и продвигаться к началу матрицы), мы создаем метод, который вначале вызывает сам себя, а затем записывает данные, соответствующие текущей позиции. Необходимо обеспечить прерывание выполнения рекурсивной подпрограммы. Это соответствует случаю, когда подпрограмма вызывается для ячейки (0,0). В этом случае никакие данные не записываются в файл. Если индекс строки То равен нулю, мы выполняем рекурсивный вызов, перемещаясь вверх по матрице (индекс строки From уменьшается), и предпринимаемым действием должно быть удаление символа из строки From. Если индекс строки From равен нулю, мы выполняем рекурсивный вызов, перемещаясь по матрице влево, и тогда действием является ставка текущего символа в строку То. И, наконец, если оба индекса не равны нулю, мы находим соответствующую ячейку в матрице, выполняем рекурсивный вызов и записываем действие в файл. Перемещению вниз соответствует удаление, перемещению вправо - вставка, перемещению по диагонали - ни одно из упомянутых действий (символ "переносится" из одной строки в другую). Для обозначения удаления мы будем использовать стрелку, указывающую вправо (-> ), а для обозначения вставки - стрелку, указывающую влево (<-). Перенос символа не обозначается.