Джулиан Бакнелл - Фундаментальные алгоритмы и структуры данных в Delphi

Листинг 8.24. Интеллектуальная подпрограмма IsRed

function IsRed(aNode : PtdBinTreeNode): boolean;

begin

if (aNode = nil) then

Result := false else

Result := aNode^.btColor = rbRed;

end;

По сравнению со вставкой, удаление из красно-черного дерева сопряжено с множеством особых случаев и его может быть трудно отследить.

Как обычно, при использовании деревьев бинарного поиска, начнем с поиска узла, который требуется удалить. Как и ранее, возможны три начальных случая: узел не имеет дочерних узлов (или, применяя терминологию, принятую в красно-черных деревьях, оба его дочерних узла являются внешними);

узел имеет один реальный дочерний узел и один внешний дочерний узел;

и, наконец, узел имеет два реальных дочерних узла. Удаление узла выполняется так же, как это делалось в стандартном неокрашенном дереве бинарного поиска.

Теперь рассмотрим эти три случая с точки зрения красно-черных деревьев. Первый случай - узел с двумя внешними дочерними узлами (т.е. с нулевыми связями). В соответствии с правилом 1, эти два дочерних узла считаются черными. Однако узел, который нужно удалить, может быть красным или черным. Предположим, что он красный. Удаляя его, мы заменяем дочернюю связь родительского узла нулевым указателем - иначе говоря, внешним черным узлом. Однако мы не изменили количество черных узлов от нового внешнего узла до корневого узла, по сравнению с существовавшими до этого двумя путями. Следовательно, правило 2 по-прежнему выполняется. Очевидно, что правило 3 также не нарушается (мы удаляем красный узел, поэтому никакие проблемы в отношении соблюдения этого правила не возникают). Таким образом, после удаления бинарное дерево остается красно-черным. Эта возможность представлена первым преобразованием на рис. 8.10.

А как насчет второй возможности (когда удаляемый узел окрашен в черный цвет)? Что ж, в этом случае правило 2, сформулированное для черных узлов, неизбежно нарушается. Количество черных узлов в пути до корневого узла уменьшается на 1. Возникающая в результате такого преобразования проблема проиллюстрирована на нижней части рисунка 8.10. Мысленно заложим в этом месте закладку и рассмотрим другие случаи.

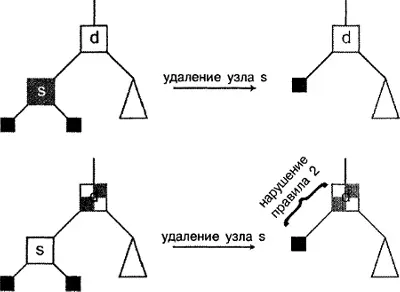
Рисунок 8.10. Удаление узла, имеющего два внешних дочерних узла

Второй случай удаления - удаление узла, который имеет один реальный дочерний узел и один внешний дочерний узел. Предположим, что удаляемый узел является красным. Его единственный реальный дочерний узел будет черным. Можно удалить узел и заменить его единственным дочерним узлом. Это не приведет к нарушению правила 2, - в конечном счете, мы удаляем красный узел, - а правило 3 в данном случае не затрагивается, следовательно, дерево остается красно-черным. Этот случай представлен первым преобразованием на рис. 8.11.

Теперь предположим, что удаляемый узел является черным. Единственный дочерний узел может быть красным или черным. Предположим, что он красный. Правило 2 неизбежно нарушается, поскольку мы удаляем черный узел, а правило 3 может быть нарушено, так как новый родительский узел красного дочернего узла может также оказаться красным. Однако этот случай достаточно прост: нужно просто перекрасить красный дочерний узел в черный цвет при перемещении его вверх для замещения удаленного узла. В результате этого простого действия мы снова добиваемся выполнения правила 2, а правило 3 в данном случае не затрагивается. Дерево снова становится красно-черным. Тот случай представлен вторым преобразованием, показанным на рис. 8.11.

Однако случай, когда единственный дочерний узел является черным, сложнее третье преобразование (на рис. 8.11). Что ж, запомним о существовании этой проблемы и рассмотрим третий, он же и последний, случай удаления.

В действительности заключительный случай удаления из дерева бинарного поиска не отличается от двух уже рассмотренных, поскольку, если помните, мы меняем местами узел, который нужно было бы удалить, с наибольшим узлом из левого дочернего дерева, а затем удаляем этот второй узел вместо первого. Этот второй узел будет соответствовать либо первому, либо второму случаю удаления, поэтому две проблемы, решение которых мы отложили, придется решать раньше, чем мы полагали.

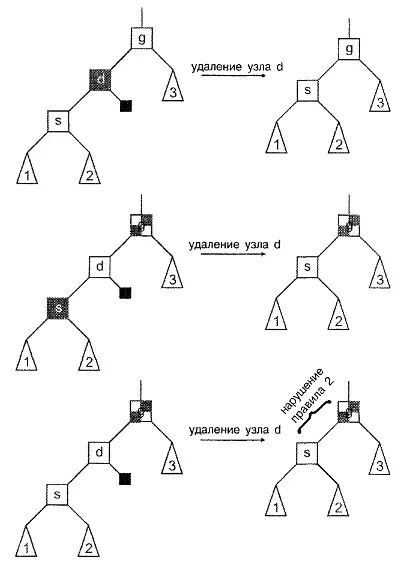
Рисунок 8.11.