Джулиан Бакнелл - Фундаментальные алгоритмы и структуры данных в Delphi

Итак, перенесем свое внимание двумя уровнями выше, примем, что узел g является новым узлом и посмотрим, нарушили ли мы какие-либо правила. Иначе говоря, снова применим рассмотренный алгоритм, но на этот раз начнем рассмотрение с узла g. Два возможных случая показаны на рис. 8.9 (естественно, могут существовать и два случая, являющиеся зеркальными отражениями представленных, но они не показаны). В обоих результирующих деревьях узел g помечен тремя восклицательными знаками, указывающими, что он может нарушать одно из двух правил, и что необходимо продолжать процесс, снова повторяя действия алгоритма.

Не прибегая к подробным математическим выкладкам, отметим, что подобно случаю применения простого бинарного дерева, алгоритм вставки в красно-черное дерево является алгоритмом типа O(log(n)), хотя в этом случае постоянный коэффициент имеет большее значение, поскольку приходится учитывать возможные повороты и повышение ранга узлов.

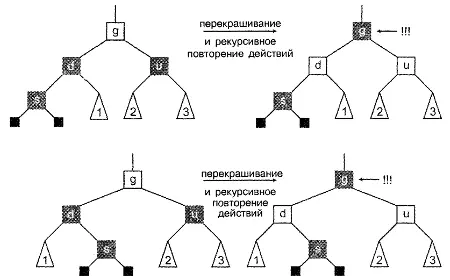
Рисунок 8.9. Балансировка после вставки: два рекурсивных случая

Код реализации этого алгоритма вставки и балансировки приведен в листинге 8.23. Метод содержит внутренний цикл, выход из которого выполняется, когда баланс дерева восстановлен. В начале цикла предполагается, что балансировка дерева должна быть выполнена в данном цикле, и что перемещение по дереву вверх должно выполняться только в том случае, если мы уверены, что снова будем выполнять цикл. В остальном приведенный код служит достаточно точным представлением алгоритма вставки в красно-черное дерево. Единственный неприятный момент - необходимость поддержания информации о том, являются ли определенные узлы левыми или правыми дочерними узлами своих родительских узлов.

Листинг 8.23. Вставка в красно-черное дерево

procedure TtdRedBlackTree.Insert(aItem : pointer);

var

Node : PtdBinTreeNode;

Dad : PtdBinTreeNode;

Grandad : PtdBinTreeNode;

Uncle : PtdBinTreeNode;

OurType : TtdChildType;

DadsType : TtdChildType;

IsBalanced : boolean;

begin

{вставить новый элемент, вернуться к вставленному узлу и его связям с родительским узлом}

Node := bstInsertPrim(aItem, OurType);

{окрасить его в красный цвет}

Node^.btColor := rbRed;

{продолжать применение в цикле алгоритмов балансировки при вставке в красно-черное дерево до тех пор, пока дерево не окажется сбалансированным}

repeat

{предположим, что дерево сбалансировано}

IsBalanced :=true;

{если узел является корневым, задача выполнена и дерево сбалансировано, поэтому будем считать, что мы находимся не в корневом узле}

if (Node <> FBinTree.Root) then begin

{поскольку мы находимся не в корневом узле, необходимо получить родительский узел данного узла}

Dad := Node^.btParent;

{если родительский узел черный, задача выполнена и дерево сбалансировано, поэтому будем считать, что родительский узел красный}

if (Dad^.btColor = rbRed) then begin

{если родительский узел является корневым, достаточно перекрасить его в черный цвет, и задача будет выполнена}

if (Dad = FBinTree.Root) then

Dad^.btColor := rbBlack {в противном случае родительский узел, в свою очередь, имеет родительский узел}

else begin

{получить прародительский узел (он должен быть черным) и перекрасить его в красный цвет}

Grandad := Dad^.btParent;

Grandad^.btColor := rbRed;

{получить узел, соответствующий понятию дяди}

if (Grandad^.btChild[ctLeft] = Dad) then begin

DadsType := ctLeft;

Uncle := Grandad^.btChild[ ctRight ];

end

else begin

DadsType := ctRight;

Uncle := Grandad^.btChild[ ctLeft ];

end;

{если дядя тоже имеет красный цвет (обратите внимание, что он может быть нулевым!), окрасить родительский узел в черный цвет, дядю в черный цвет и повторить процесс, начиная с прародительского узла}

if IsRed(Uncle) then begin

Dad^.btColor :=rbBlack;

Uncle^.btColor := rbBlack;

Node := Grandad;

IsBalanced := false;

end

{в противном случае дядя окрашен в черный цвет?}

else begin

{если текущий узел имеет такие же отношения со своим родительским узлом, какие его родительский узел имеет с прародительским (т.е. они оба являются либо левыми, либо правыми дочерними узлами), нужно окрасить родительский узел в черный цвет и повысить его ранг. Задача выполнена}

OurType := GetChildType(Node);

if (OurType = DadsType) then begin

Dad^.btColor := rbBlack;

rbtPromote(Dad);

end

{в противном случае необходимо окрасить узел в черный цвет и повысить его ранг посредством применения спаренного двустороннего поворота; задача выполнена}

else begin

Node^.btColor :=rbBlack;

rbtPromote(rbtPromote(Node));

end;

end;

end;

end;

end;

until IsBalanced;

end;

Необходимо принимать во внимание один небольшой нюанс: следует проверять цвета узлов. Некоторые из узлов, которые мы будем проверять, будут внешними, т.е. нулевыми. Для повышения читабельности кода я написал небольшую подпрограмму IsRed, которая выполняет проверку на наличие нулевого узла (возвращая значение false), прежде чем выполнять проверку поля цвета узла.