Джулиан Бакнелл - Фундаментальные алгоритмы и структуры данных в Delphi

Начнем с того, что окрасим его в красный цвет. Как это сказывается на соблюдении правил, определенных для красно-черных деревьев? Во-первых, условие для черных узлов по-прежнему выполняется: мы заменяем черный внешний узел красным узлом и двумя черными внешними узлами. Путь от каждого из двух новых внешних узлов до корневого узла по-прежнему содержит столько же черных узлов, сколько и путь от замещенного внешнего узла до корневого узла. А как насчет условия, определенного для красных узлов? Продолжает ли оно выполняться? Возможно, да, а, возможно, и нет. Если новый узел является корневым, и, следовательно, не имеет родительского узла, созданное дерево остается красно-черным (в действительности, при желании новый узел можно было бы перекрасить в черный цвет, и при этом дерево осталось бы красно-черным). Если же новый узел не является корневым, он будет иметь родительский узел. Если этот родительский узел черный, правило 3, определенное для красных узлов, остается применимым, и дерево по-прежнему является красно-черным. Если родительский узел нового узла является корневым, то, чтобы дерево осталось красно-черным, достаточно при необходимости перекрасить родительский узел в черный цвет. (Фактически, в красно-черном дереве, если оба дочерних узла корневого узла являются черными, корневой узел может быть как красным, так и черным - это никак не сказывается на соблюдении правил.)

Если родительский узел нового узла не является корневым и окрашен в красный цвет, мы получаем два следующие друг за другом красные узла. При этом правило, определенное для красных узлов, нарушается, и для воссоздания красно-черного дерева эту проблему придется решить.

В этой ситуации возможны несколько вариантов. Чтобы было проще понять происходящее, вначале присвоим имена ряду узлов. После этого можно будет описать некоторые преобразования, которые потребуется выполнить, чтобы вернуть дерево в красно-черное состояние.

Назовем новый узел s (от son - сын), его родительский узел d (от dad - отец), родительский узел родительского узла g (granddad - дед), а родственный с родительским узлом - и (uncle - дядя). Непосредственно после добавления узла s возникает следующая ситуация: узлы s и d являются красными (что является нарушением правила 2), узел g должен быть черным (согласно правилу 2), а узел и может быть либо красным, либо черным.

Вначале предположим, что узел и является черным. Для достижения поставленной цели достаточно выполнить либо одиночный поворот, либо спаренный двусторонний поворот, а затем перекрасить некоторые узлы. В первом случае, который на рис. 8.8 представлен первым преобразованием, мы выполняем поворот узла d вправо на место узла g, чтобы g стал дочерним узлом узла d. Затем мы перекрашиваем узел d в черный цвет, a g - в красный. Во втором случае (нижнее преобразование на рис. 8.8) мы выполняем спаренный двусторонний поворот, чтобы поместить узел s на место g, а затем перекрашиваем узел s в черный цвет, a g - в красный. Обратите внимание, что абсолютно не важно, является ли узел и внешним или внутренним; достаточно, чтобы он был черным.

Естественно, возможны еще два случая, представляющие собой зеркальное отражение рассмотренных, однако мы не будем их рассматривать. На рисунке 8.8 легко видеть, что теперь условие, определенное для красных узлов, удовлетворено, и что операции поворота и перекрашивания не нарушают условие, определенное для черных узлов.

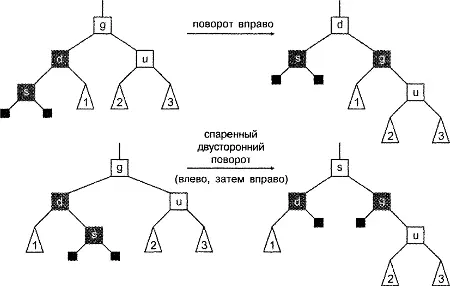
Рисунок 8.8. Балансировка после вставки: два простых случая

Этот случай был простым. Теперь рассмотрим более сложный. Предположим, что узел и, дядя нового узла, также окрашен в красный цвет. Первый шаг прост: мы перекрашиваем узлы d и u в черный цвет, а g в красный. Условие для черных узлов по-прежнему выполняется, но, похоже, мы ухудшили общую ситуацию, поскольку условие, определенное для красных узлов, перестало выполняться. Вместо того чтобы признать, что узел s нарушает условие, определенное для красных узлов, мы предположили, каким мог бы быть узел g. В конце концов, родительский узел узла g мог бы быть и красным. Иначе говоря, в действительности эта операция перекрашивания не решает никаких проблем. Мы просто отложили решение проблемы на неопределенный срок. Но действительно ли ситуация ухудшилась? Посмотрите, что мы сделали: мы переместили проблемный узел вверх по дереву. Перемещение вверх ограничено в пространстве, поскольку со временем мы натолкнемся на корневой узел.