Михаил Краснов - Графика DirectX в Delphi

type

TRGB = packed record // Запись цвета

R, G, В : BYTE;

end;

const

Size =2; // Размер отдельного квадратика, "пиксела"

Fade =4; // Степень затухания пламени

NumX = 150; // Количество квадратиков по горизонтали

NumY = 150; // Количество квадратиков по вертикали

var

Fire : Array [L.NumX, L.NumY + 1] of TRGB; // Цвета узлов сетки

PreF : Array [L.NumX] of TP.GB; // Вспомогательный массив первой строки

Angle : Single = 0.0; // для движения падающей точки

ParticleX : Integer =0; // Координаты точки

ParticleY : Integer = NumY;

Следующая пользовательская функция выводит один квадрат, цвета углов которого задаются текущими значениями элементов массива Fire:

function TfrmDSD.DrawPix(const inX, inY : Integer) : HRESULT;

var

pVertices : PByte;

hRet : HRESULT;

begin

with VPoints [0] do begin // Левый нижний угол квадрата

X := inX * Size;

Y := 300 - inY * Size; // Переворачиваем ось Y

Color := D3DCOLOR_XRGB(Fire[inX, inY + 1].R, Fire[inX, inY + 1].G,

Fire[inX, inY + 1].B);

end;

with VPoints [1] do begin // Левый верхний угол квадрата

X := inX * Size;

Y := 300 - (inY + 1) * Size;

Color := D3DCOLOR_XRGB(Fire[inX, inY].R, Fire[inX, inY].G,

Fire[inX, inY].B); end; with VPoints [2] do begin // Правый нижний угол квадрата

X := (inX + 1) * Size;

Y := 300 - inY * Size;

Color := D3DCOLOR_XRGB(Fire[inX + 1, inY + 1].R, Fire[inX + 1,

inY + 1].G, Fire[inX + 1, inY + 1].B);

end;

with VPoints [3] do begin // Правый верхний угол квадрата

X := (inX + 1) * Size;

Y := 300 - (inY + 1) * Size;

Color := D3DCOLOR_XRGB(Fire[inX + 1, inY].R, Fire[inX + 1, inY].G,

Fire[inX + 1, inY].B);

end;

hRet := FD3DVB.Lock(0, SizeOf(VPoints), pVertices, 0];

if Failed (hRet) then begin

Result := hRet;

Exit;

end;

Move (VPoints, pVertices^, SizeOf(VPoints));

hRet := FD3DVB.Unlock;

if FAILED(hRet) then begin

Result := hRet;

Exit;

end;

Result := FD3DDevice.DrawPrimitive(D3DPT_TRIANGLESTRIP, 0, 2);

end;

Для формирования собственно пламени последняя строка инициализируется случайным оттенком красного, в последующих пикселах цвет затухает, а для создания эффекта размытия языков пламени используется простой прием с усреднением цветов соседних точек:

procedure TfrmD3D.DrawFire;

i, j : Integer;

f : Byte;

begin

// Инициализация последней строки экрана

for i := 2 to NumX-1 do begin

f := random(255) ;

PreF[i].R := 255;

PreF[i].G := trunc (f / 1.4);

PreF[i] . := f div 2;

end;

// Заполняем в массиве Fire последнюю строку

// усредненными значениями соседних элементов

PreF '" for i := 2 to NumX - 1 do begin

Fire[i, 1}.R := (PreF[i - 1] .R 4- PreF[i 4- 1} .R + PreF[i] .R) div 3; $; Fire[i, 1].G := (PreF[i - 1] .G + PreF[i + 1] .G + PreF[i] .G) div 3; Fire[i, 1].B := (PreF[i - 1].B + PreF[i + 1].B + PreF[i].B) div 3; end;

// Смешивание, усреднение значений пикселов по экрану for j := NumY - 1 downto 2 do for i := 2 to NumX - 1 do begin

Fire[i,j].R := (Fire[i-1, j].R + Fire[i+1, j].R + Fire[i,j].R +

Fire[i-1, j-1].R + Fire[i+1, j-1].R +

Fire[i, j-1].R) div 6;

Fire[i,j].G := (Fire[i-1, j].G + Fire[i+1, j].G + Fire[i,j].G +

Fire[i-1, j-1].G + Fire[i+l, j-1].G +

Fire[i, j-1].G) div 6;

Fire[i,j].B := (Fire[i-1, j].B + Fire[i+1, j].B +

Fire[i,j].B + Fire[i-1, j-1].B + Fire[i+1, j-1].B +

Fire[i, j-1].B) div 6;

end;

// Квадратик, соответствующий падающей частице for j := ParticleY - 1 to ParticleY do

for j := ParticleX - 1 to

ParticleX do begin

Fire[i, j].R := 255;

Firefi, j].G := 0;

Fire[i, j].B := 0;

end;

// Вывод квадратиков содержимого экрана

for j := 2 to NumY - 1 do

for i := 2 to NumX - 1 do

DrawPix (i - 1, j - 1) ;

// Затухание оттенков по мере подъема языков пламени

for j := NumY downto 2 do

for i := 1 to NumX do begin

if Fire[i, j - 1J.R >= Fade

then Firefi, j].R = Firefi, j - 1].R- Fade

else Firefi, j].R = 0;

if Firefi, j - 1].G >= Fade

then Firefi, j].G = Firefi, j - 1].G - Fade

else Firefi, j].G = 0;

if Firefi, j - 1].B >= Fade

then Firefi, j].B = Firefi, j - 1].B - Fade

else Firefi, j].B = 0;

end;

end;

Последний примитив, связанный с флагом DSDPTJTRIANGLEFAN, также предназначен для построения группы связанных треугольников, но данные потока здесь трактуются немного иначе, чем в предыдущем случае: вторая, третья и первая вершины определяют первый треугольник, третья, четвертая и первая ассоциированы со вторым треугольником, и т. д. То есть треугольники связаны, подобно раскрою зонтика или веера. Первая вершина потока ассоциирована с центральной точкой (рис. 7.17), а порядок перечисления вершин особенно важен для режима отключенной интерполяции цветов вершин.

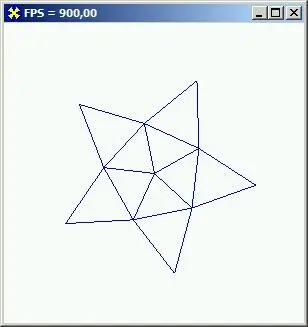
По такой схеме удобно строить конусы и пирамиды, а для плоскостных построений - выпуклые многоугольники, эллипсы и окружности. Приведу тривиальный пример на этот случай (проект из каталога Ех27).

Значение константы Level задает степень разбиения полного круга, количество вершин нам требуется на пару больше этого значения:

const

Level = 255;

var

VPoints : Array [0..Level + 1] of TCUSTOMVERTEX;

Нервая вершина массива хранит координаты центральной точки круга, все детальные равномерно располагаются на его границе:

const

Step = 2 * Pi / Level;

with VPoints [0] do begin // Первая точка - центр круга

х := 150;

Y := 150;

Color := D3DCOLOR_XRGB(0, 0, 0);

end;

If for i := 1 to Level + 1 do // Точки на краю круга

with VPoints [i] do begin

X := 150 + cos (Angle + i * Step) * Radius;