Figure 16.3 shows the resource allocation graph. The graph represents the following:
· a circle represents a resource,
· a square represents a task or thread of execution,
· an arrow going from a task to a resource indicates that the task wants the resource, and
· an arrow going from a resource to a task indicates that the task currently holds the resource.
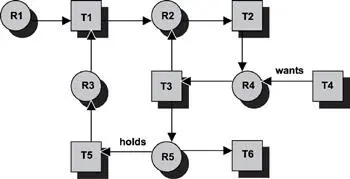
Figure 16.3: Current state of resource allocations and requests.
In the following discussions, node refers either to the circle (resource) or the square (task) in Figure 16.3. Arc refers to the arrow. The deadlock detection algorithm can be stated in these seven steps:
1. Make a list of all the nodes, N , from the graph.
2. Pick a node from N . Create another list, L , initially empty, which is used for the graph traversal.
3. Insert the node into L and check if this node already exists in L . If so, a cycle exists; therefore, a deadlock is detected, and the algorithm terminates. Otherwise, remove the node from N .
4. Check whether any un-traversed outgoing arcs from this node exist. If all of the arcs are traversed, go to step 6.
5. Choose an un-traversed outgoing arc originating from the node and mark the arc as traversed. Follow the chosen arc to the new node and return to step 3.
6. At this stage, a path in the graph terminates, and no deadlocks exist. If more than one entry is in L , remove the last entry from L . If more than one entry remains in L , make the last entry of L the current node and go to step 4.
7. If the list N is not empty, go to step 2. Otherwise, the algorithm terminates, and no deadlocks exist in the system.
The actual implementation from step 3 to step 6 translates into a depth first search of the directed graph.
Applying this algorithm to the system depicted in Figure 16.3 provides the following:
Step 1: N = {R1, T1, R2, T2, R3, T3, R4, T4, T5, R5, T6}
Step 2: L = {‹ empty ›}; pick node R1
Step 3: L = {R1}; no cycles are in L; N = {T1, R2, T2, R3, T3, R4, T4, T5, R5, T6}
Step 4:R1 has one outgoing arc
Step 5:Mark the arc; reaches node T1; go back to step 3
Step 3: L = {R1, T1}; N = {R2, T2, R3, T3, R4, T4, T5, R5, T6}; no cycles are in L
The algorithm continues from step 3 to step 5 and reiterates until it reaches node T3, in which the list L = {R1, T1, R2, T2, R4, T3} and the list N = {R3, T4, T5, R5, T6}. Two outgoing arcs are at node T3. When the downward arc is picked, L = {R1, T1, R2, T2, R4, T3, R5}. Two outgoing arcs are at node R5. When the rightward arc is picked, L = {R1, T1, R2, T2, R4, T3, R5, T6}.
Step 4:T6 does not have any outgoing arcs; continue to step 6
Step 6:Remove T6 from the list L; L = {R1, T1, R2, T2, R4, T3, R5}; return to step 4
Step 4:Pick the unmarked leftward arc at R5
Step 5:Mark the arc; reaches node T5; return to step 3
Step 3: L = {R1, T1, R2, T2, R4, T3, R5, T5}; N = {R3, T4}; no cycles are in L
Step 4:Pick the only outgoing arc at T5
Step 5:Mark the arc; reaches node R3; go back to step 3
Step 3: L = {R1, T1, R2, T2, R4, T3, R5, T5, R3}; N = {T4}; still no cycles are in L
Step 4:Pick the only outgoing arc at R3
Step 5:Mark the arc; reaches node T1; go back to step 3
Step 3: L = {R1, T1, R2, T2, R4, T3, R5, T5, R3, T1}; Node T1 already exists in L . A cycle is found in the graph, and a deadlock exists. The algorithm terminates.
The deadlock set is comprised of the entire nodes enclosed by the two occurrences of node T1 inclusively. Therefore, the discovered deadlock set is {T1, R2, T2, R4, T3, R5, T5, R3}. One thing worth noting is that the algorithm detects deadlocks if any exist. Which deadlock is detected first depends on the structure of the graph. Closer examination of the resource graph reveals that another deadlock exists. That deadlock set is {R2, T2, R4, T3}. At node T3 if the upward arc is chosen first instead of the downward arc, this later deadlock occurrence would be discovered, and the algorithm would terminate much sooner.
Multi-Instance Resource Deadlock Detection
The deadlock detection algorithm takes a different approach for systems with multiple instances of each resource type, and tasks make resource requests following the AND model. An underlying assumption is that a resource allocation system is present. The resource allocation system is comprised of a set of different types of resources, R1, R2, R3,…, R n . Each type of resource has a fixed number of units. The resource allocation system maintains a resource allocation table and a resource demand table.
Each row of tables C and D represents a task T. Each column of tables C and D is associated with a resource type. C is the resource allocation table representing resources already allocated. D is the resource demand table representing additional resources required by the tasks.
| N = Total System Resources Table |
N 1 |
N 2 |
N 3 |
… |
N k |
where N i is the number of units of resource type R i for all i where {1 ≤ i ≤ k }.
| A = Available System Resources Table |
A 1 |
A 2 |
A 3 |
… |
A k |
where A i the number of units remaining for resource type R i available for allocation.
| C = Tasks Resources Assigned Table |
C 11 |
C 12 |
C 13 |
… |
C 1 k |
| C 21 |
C 22 |
|
… |
C 2 k |
| … |
|
|
… |
|
| C m 1 |
|
|
… |
C mk |
| D = Tasks Resources Demand Table |
D 11 |
D 12 |
D 13 |
… |
D 1 k |
| D 21 |
D 22 |
|
… |
D 2 k |
| … |
|
|
… |
|
| D m 1 |
|
|
… |
D mk |
For example in table C, there are C 11units of resource R1, C 12units of resource R2, and so on, which are allocated to task T1. Similarly, there are C 21units of resource R1, C 22units of resource R2, and so on, which are allocated to task T2. For example in table D, task T1 demands additional D 11units of resource R1, additional D 12units of resource R2, and so on, in order to complete execution.
The deadlock detection algorithm is as follows:
1. Find a row i in table D, where D ij ‹ A j for all 1 ≤ j ≤ k . If no such row exists, the system is deadlocked, and the algorithm terminates.
2. Mark the row i as complete and assign A j = A j + D ij for all 1 ≤ j ≤ k .
3. If an incomplete row is present, return to step 1. Otherwise, no deadlock is in the system, and the algorithm terminates.
Step 1 of the algorithm looks for a task whose resource requirements can be satisfied. If such a task exists, the task can run to completion. Resources from the completed task are freed back into the resource pool, which step 2 does. The newly available resources can be used to meet the requirements of other tasks, which allow them to resume execution and run to completion.
Читать дальше













