John Crisp - Introduction to Microprocessors and Microcontrollers

Start from the left-hand end and invert each bit until you come to the last figure 1. Don’t invert this figure and don’t invert anything after it.

Example 1

What is –24 10expressed as an 8-bit two’s complement binary number?

1 Change the 24 10into binary. This will be 11000.

2 Add leading zeros to make it an 8-bit number. This is now 00011000.

3 Now start inverting each bit, working from the left until we come to the last figure ‘1’. Don’t invert it, and don’t invert the three zeros that follow it.

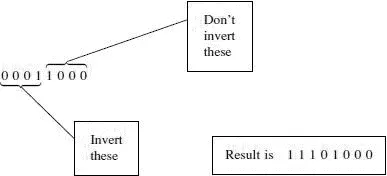
Example 2

What is –100 10expressed as a 16-bit two’s complement binary number?

1 Convert the 10010 into binary. This gives 1100100 2.

2 Add nine leading zeros to make the result the 16-bit number 0000000001100100.

3 Now, using the quick method, find the two’s complement:

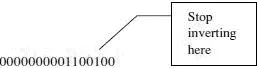
The result is 1111 1111 1001 1100

Example 3

Find the value of 1011 0111 2–00 1011 2using two’s complement addition.

1 The second number has only six bits so add two zeros on the lefthand end to give 1011 0111–0000 1011.

2 Invert each bit in the number to be subtracted to find the one’s complement. This changes the 00001011 to 11110100.

3 Add 1 to give the two’s complement: 11110100+1=11110101 (or do it the quick way).

4 Add the first number to the two’s complement of the second number:

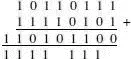
5 The result so far is 110101100 which includes that extra carry so we cross off the msb to give the final answer of 10101100 2.

Eight-bit numbers are limited to a maximum value of 11111111 2or 255 10. So, 0–255 means a total of 256 different numbers. Not very many. 32-bit numbers can manage about 4¼ billion. This is quite enough for everyday work, though Bill Gates’ bank manager may still find it limiting. The problem is that scientific studies involve extremely large numbers as found in astronomy and very small distances as in nuclear physics.

So how do we cater for these? We could wait around for a 128-bit microprocessor, and then wait for a 256-bit microprocessor and so on. No, really, the favorite option is to have a look at alternative ways of handling a wide range of numbers. Rather than write a number like 100 we could write it as 1×10². Written this way it indicates that the number is 1 followed by two zeros and so a billion would be written as 1×10 9. In a similar way, 0.001 is a 1 preceded by two zeros would be written as 1×10 –3and a billionth, 0.000000001, would be 1×10 –9. The negative power of ten is one greater than the number of zeros. By using floating point numbers, we can easily go up to 1×10 99or down to 1×10 –99without greatly increasing the number of digits.

Fancy names

Normalizing

Changing a number from the everyday version like 275 to 2.75×10² is called normalizing the number. The first number always starts with a single digit between 1 and 9 followed by a power of ten. In binary we do the same thing except the decimal point is now called a binary point and the first number is always 1 followed by a power of two as necessary.

Three examples

1 Using the same figure of 275, this could be converted to 100010011 in binary. This number is normalized to 1.00010011×2 8.

2 A number like 0.0001001 2will have its binary point moved four places to the right to put the binary point just after the first figure 1 so the normalized number can be written as 1.001×2 –4.

3 The number 1.101 2is already normalized so the binary point does not need to be moved so, in a formal way, it would be written as 1.101×2 0.

A useless fact

Anything with a power of zero is equal to 1. So 2 0=1, 10 0=1. It is tempting but total nonsense to use this fact to argue that since 2 0=1 and 10 0=1 then 2 must equal 1 0!

Terminology

There are some more fancy names given to the parts of the number to make them really scary.

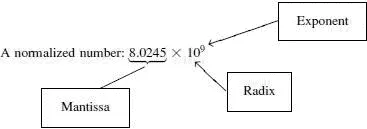
The exponent is the power of ten, in this example, 9. The mantissa, or magnitude, is the number, in this case 8.0245. The radix is the base of the number system being used, 2 for binary, 16 for hex, 10 for decimal.

Storing floating point numbers

In a microprocessor, the floating point is a binary number. Now, in the case of a binary number, the mantissa always starts with 1 followed by the binary point. For example, a five digit binary mantissa would be between 1.0000 and 1.1111.

Since all mantissas in a binary system start with the number 1 and the binary point, we can save storage space by missing them out and just assuming their presence. The range above would now be stored as 0000 to 1111.

It is usual to use a 32-bit storage area for a floating point number. How these 32 bits are organized is not standardized so be careful to check before making any assumptions. Within those 32 bits, we have to include the exponent and the mantissa which can both be positive or negative. One of the more popular methods is outlined below.

Bit 0 is used to hold the sign-bit for the mantissa using the normal convention of 0 = positive and 1 = negative.

Bits 1–23 hold the mantissa in normal binary.

Bits 24–31 hold the exponent. The eight digits are used to represent numbers from –127 to +128 using either two’s complement numbers or excess-127 notation.

We have already met two’s complement numbers earlier in this chapter so we will look at excess-127 notation now.

Excess-127 notation

This is very simple, despite its impressive name. To find the exponent just add 127 to its value then convert the result to binary. This addition will ensure that all exponents have values between 0 and 255, i.e. all positive values.

Example

If the exponent is –35 then we add 127 to give the result 92, which we can then convert to binary (01011100).

When the value is to be taken out of storage and converted back to a binary number, the above process is reversed by subtracting the 127 from the exponent.

The mantissa can go as high as 1.1111 1111 1111 1111 1111 111 2. To the right of the binary point the decimal equivalents are values of 1.5+0.25+0.125+0.0625 etc. Adding these up gives a total that is virtually 2 – but not quite. The larger the number of bits in the mantissa, the more accuracy we can expect in the result. The exponent has eight bits so it can range from –127 to +128 giving a maximum number of 1×2 128which is approximately 3.4×10 38. The accuracy is limited by the number of bits that can be stored in the mantissa, which in this case is 23 bits.

If we want to keep to a total of 32 bits, then we have a trade-off to consider. Any increase in the size of the exponent, to give us larger numbers, must be matched by reducing the number of bits in the mantissa that would have the effect of reducing the accuracy. Floating point operations per second (FLOPS) is one of the choices for measuring speed.