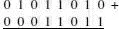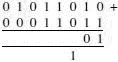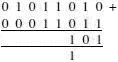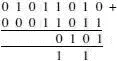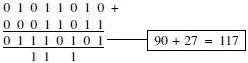There was a time when we had to enter binary and get raw binary answers but thankfully, those times have gone. Everything was definitely NOT better in the ‘good old days’.
The form binary numbers take inside of the microprocessor depends on the system design and the work of the software programmers. We will take a look at the alternatives, starting with negative numbers.
In real life, it is easy, we just put a – symbol in front of the number and it is negative so +4 becomes –4. Easy, but we don’t have any way of putting a minus sign inside the microprocessor. We have tried several ways round the problem.
Signed magnitude numbers
The first attempt seemed easy but it was false optimism. All we had to do was to use the first bit (msb) of the number to indicate the sign 1 = minus, 0 = plus.
This had two drawbacks.
1 It used up one of the bits so an 8-bit word could now only hold seven bits to represent numbers and one bit to say ‘plus’ or ‘minus’. The seven bits can now only count up to 1111111 2=127 whereas the eight bits should count to 255.
2 If we added two binary numbers like +127 and +2, we would get:
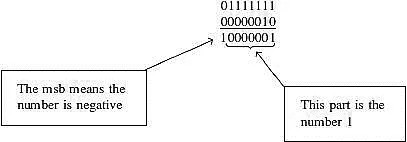
The msb (most significant bit) of 1 means it is a minus number and the actual number is 0000001=1. So the final result of +127+2 is not 129 but minus 1.
When we use a microprocessor to handle arithmetic with these problems, we can ensure that the microprocessor can recognize this type of accidental negative number. We can arrange for the microprocessor to compensate for it but it is rather complicated and slow.
Luckily, a better system came along which has stood the test of time, having been used for many years.
Complementary numbers
This has two significant advantages:
1 It allows the full number of bits to be used for a number so an 8-bit word can count from 0 to 11111111 2or 255.
2 It is easy to implement with addition and subtraction using substantially the same circuitry.
So, how do we manage to use all eight bits for numbers yet still be able to designate a number positive or negative?
That’s clever. We will start by looking at positive numbers first because it is so easy. All positive numbers from 0 to 255 are the same as we get by simply converting denary to binary numbers. So that’s done.
Addition
Example
Add 01011010 + 00011011.
The steps are just the same as in ‘normal’ denary arithmetic. Step 1 Lay them out and start from the lsb (least significant bit) or right-hand bit
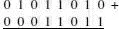
Add the right-hand column and we have 0+1=1. So we have

Step 2 Next we add the two 1s in the next column. This results in 2, or 10 in binary. Put the 0 in the answer box and carry the 1 forward to the next column
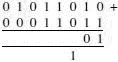
Step 3 The next column is easy 0+0+1=1
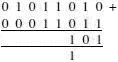
Step 4 The next line is like the second column, 1+1=10. This is written as an answer of 0 and the 1 is carried forward to the next column
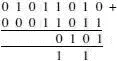
Step 5 We now have 1 in each row and a 1 carried forward so the next column is 1+1+1=3 or 11 in binary. This is an answer of 1 and a 1 carried forward to the next column

Step 6 The next column is 0 + 0 + 1 = 1, and the next is 1 + 0 = 1 and the final bit or msb is 0 + 0 = 0, so we can complete the sum
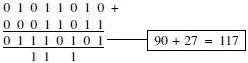
Subtraction
Here is a question to think about: What number could we add to 50 to give an answer of 27? In mathematical terms this would be written as 50+ x =27.
What number could x represent? Surely, anything we add to 50 must make the number larger unless it is a negative number like –23:
50 + (–23) = 27
The amazing thing is that there is a number that can have the same effect as a negative number, even though it has no minus sign in front of it. It is called a ‘two’s complement’ number.
Our sum now becomes:
50 + (the two’s complement of 23) = 27
This magic number is the two’s complement of 23 and finding it is very simple.
How to find the two’s complement of any binary number
Invert each bit, then add 1 to the answer
All we have to do is to take the number we want to subtract (in its binary form) and invert each bit so every one becomes a zero and each zero becomes a one. Note: technically the result of this inversion is called the ‘one’s complement’ of 23. The mechanics of doing it will be discussed in the next chapter but it is very simple and the facility is built into all microprocessors at virtually zero cost.
Converting the 23 into a binary number gives the result of 00010111 2(using eight bits). Then invert each bit to give the number 11101000 2then add 1. The resulting number is then referred to as the ‘two’s complement’ of 23.

Introduction to Microprocessors and Microcontrollers In this example, we used 8-bit numbers but the arithmetic would be exactly the same with 16 bits or indeed 32 or 64 bits or any other number.
Doing the sum
We now simply add the 50 and the two’s complement of 23:
50 + (the two’s complement of 23) = 27
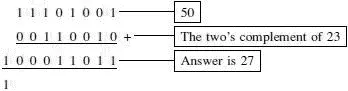
The answer is 100011011.
Count the bits. There are nine! We have had a carry in the last column that has created a ninth column. Inside the microprocessor, there is only space for eight bits so the ninth one is not used. If we were to ask the microprocessor for the answer to this addition, it would only give us the 8-bit answer: 00011011 2or in denary, 27. We’ve done it! We’ve got the right answer!
It was quite a struggle so let’s make a quick summary of what we did.
1 Convert both numbers to binary.
2 Find the two’s complement of the number you are taking away.
3 Add the two numbers.
4 Delete the msb of the answer.
Done.
A few reminders
1 Only find the two’s complement of the number you are taking away – NOT both numbers.
2 If you have done the arithmetic correctly, the answer will always have an extra column to be deleted.
3 If the numbers do not have the same number of bits, add leading zeros as necessary as a first job. Don’t leave until later. Both of the numbers must have the same number of bits. They can be 8-bit numbers as we used, or 16, or 32 or anything else so long as they are equal.
Читать дальше