Александр Харчевников - Социальный метаболизм. Полилогический матричный анализ «обменных процессов» и стоимости

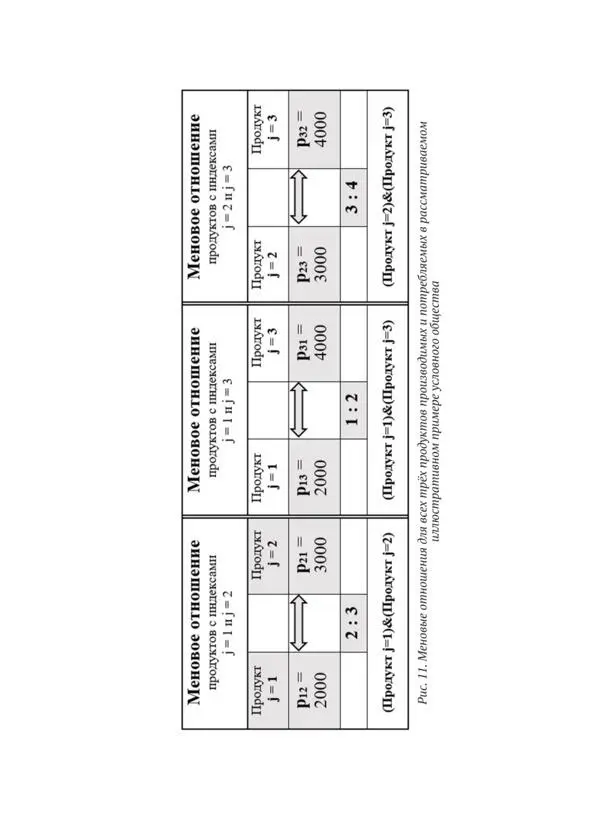
Таким образом имеем три «меновых» отношения для всех трёх продуктов производимых и потребляемых в рассматриваемом иллюстративном примере условного общества. Эти три меновых отношения представлены в таблице рисунка 11.

Выполненный анализ условного примера формирования балансовой матрицы «производство – потребление» основан на учёте целостного единства воспроизводственного процесса действительной жизни общества, «единого целого» – по К. Марксу. Он показал, что так называемое «меновое отношение» возникает не на базе «меновой стоимости товаров», которая как утверждает автор «Капитала», – «и есть их стоимость». В частности, К. Маркс так характеризует этот стоимостной остаток:

– «…одинаковой для всех призрачной предметности, простого сгустка лишенного различий человеческого труда, т. е. затраты человеческой рабочей силы безотносительно к форме этой затраты. Все эти вещи представляют собой теперь лишь выражения того, что в их производстве затрачена человеческая рабочая сила, накоплен человеческий труд. Как кристаллы этой общей им всем общественной субстанции, они суть стоимости – товарные стоимости.

…Таким образом, то общее, что выражается в меновом отношении, или меновой стоимости товаров, и есть их стоимость . Дальнейший ход исследования приведет нас опять к меновой стоимости как необходимому способу выражения, или форме проявления стоимости;…

…Как же измерять величину ее стоимости? Очевидно, количеством содержащегося в ней труда, этой «созидающей стоимость субстанции». Количество самого труда измеряется его продолжительностью, рабочим временем… » (Выделено мной. – ХАТ) [3, с. 4].

Однако, – базой возникновения менового отношения , как показывает приведённый условный пример одного цикла кругооборота (обращения) воспроизводственного процесса, является устойчивое сохранение равновесного состояния общества как единого целого , что «свойственно всякому органическому целому». При этом заметим отсутствие в приведённом анализе даже какого-либо упоминания стоимости, рабочего времени и «труда, этой „созидающей стоимость субстанции“» по Марксу.

Следовательно, можно полагать, утверждать, что полученные в приведённом примере меновые отношения есть выражение «органическим целым» общества его целостного единства. А это отторгает утверждение автора «Капитала» о стоимости, лежащей в основе менового отношения, – в основе этой «пропорции».

Так, в этой связи, изначально, К. Маркс пишет:

«Меновая стоимость прежде всего представляется в виде количественного соотношения, в виде пропорции, в которой потребительные стоимости одного рода обмениваются на потребительные стоимости другого рода, – случайного соотношения, постоянно изменяющегося в зависимости от времени и места. Меновая стоимость кажется поэтому чем-то случайным и чисто (совершенно – ХАТ) относительным, внутренняя для товара имманентная (присущая самому товару – ХАТ) меновая стоимость (valeur intrinsèque) представляет, по-видимому, бессмыслицу (представляется каким-то contradictio in adjecto [противоречием в определении] – ХАТ)» [3, с. 2].

Вместе с этим, выявленным нами отторжением стоимости, «обессмысливается» и такое заключение из политэкономии «Капитала»:

«Стоимость одного товара относится к стоимости каждого другого товара, как рабочее время, необходимое для производства первого, к рабочему времени, необходимому для производства второго. „Как стоимости, все товары суть лишь определенные количества застывшего рабочего времени“» [3, с. 5].

Наконец, как пишет К. Маркс, – «Если отвлечься от потребительной стоимости товарных тел, то у них остается лишь одно свойство, а именно то, что они – продукты труда» [3, с. 3]. Следует заметить, что этим отторгается, скорее – «ущемляется», само понятие менового отношения, так как не только «продукты труда» охватываются меновым отношением. В этой связи, но несколько позднее, мы вернёмся к указанной проблеме и, в отличие от монологического и гомогенного «Капитала», предложим эффективное гетерогенное решение на основе метатеория «Полилогия современного мира…» [13].

Изложенное выше решение для условного примера относиться к некоторому упрощённому варианту, сводящему трёхмерное пространство материального производства в координатах i, jи kк двухмерному пространству i и k. Поэтому рассмотрим более строгое математическое решение той же задачи.