Александр Александров - Исследование имени и судьбы на основе цифрового анализа

© Александров А. Ф., наследники, 2015

© ООО Группа Компаний «РИПОЛ классик», 2015

Для пользования этой книгой вам не понадобятся дополнительные знания. Можете смело открывать ее на странице с интересующим вас именем и знакомиться со всеми его особенностями, не переживая, что вы чего-то не знаете.

Начальные главы предназначены исключительно для любознательных читателей и для тех, кто уже имеет представление о цифровом анализе благодаря книгам, которые выпустило издательство РИПОЛ-классик.

Каждый читатель, знакомый с методами цифрового анализа или имеющий книги по данной системе, получает возможность проверить правильность трактовки того или иного имени, так как вся информация основана на конкретном наборе цифр, который соответствует имени, и на точных методах цифрового анализа. Эта особенность отличает настоящее издание от всех других книг, посвященных исследованию имен.

Интересно отметить, что идея установления соответствия между цифрами и буквами русского алфавита (кириллицы) не нова. Еще в древние времена на Руси были распространены всевозможные гадания по именам с использованием цифр или чисел (счета). Особенно популярной была методика, использующая соответствие между буквами и числами, так как в древнерусском языке числа обозначались буквами, что позволяло переводить запись любого имени в набор чисел, с которыми можно было производить простейшие математические действия (сложение или вычитание).

Более того, каждая буква кириллицы имела свое прочтение (словесную формулу), например, „з“ – „зело“, „в“ – „веди“, г – „глагол“ и так далее. Данная система имела одну особенность: все расшифровки имен носили религиозную направленность. Подобная трактовка мало употребительна в наше время, когда у человека имеется широчайший выбор религиозных симпатий и предпочтений и когда многие являются атеистами. Однако прежде чем приступить к разъяснению особенностей анализа имен, напомним основы цифрового анализа, которые сделают настоящую книгу доступной для всех без исключения читателей.

Допустим, дата рождения человека:

15 4 1972 (15 апреля 1972 года)

Для выполнения расчета необходимо рассматривать каждую дату рождения как набор цифр, а не чисел. Запись даты рождения производится в строгой последовательности, однозначные числа записываются без нулей перед ними:

верно – 15 4 1972, неверно – 15 04 1972;

запись: число, месяц, год (порядок не нарушать!).

Выпишем числовой ряд для выбранной даты рождения (оставив место под цифрами для новых чисел):

1 5 4 1 9 7 2

(1) (2) (3) (4)

Новые числа (1), (2), (3) и (4) запишем после их расчета.

Вычислим первое число (1).

Для расчета первого числа необходимо сложить все цифры (однозначные числа) числового ряда даты рождения.

1 + 5 + 4 + 1 + 9 + 7 + 2 = 29

Первое число (1) – 29.

Вычислим второе число (2).

Для расчета второго числа необходимо сложить цифры, из которых состоит первое число (1).

2 + 9 = 11

Второе число (2) – 11.

Если первое число однозначное, то второе число совпадает с ним, как если бы мы прибавили к первому числу ноль.

Вычислим третье число (3).

Для расчета третьего числа необходимо вычесть из первого числа (в нашем примере цифра 29) первую цифру всего ряда (в нашем примере цифра 1), умноженную на постоянный множитель – 2 (два).

29–1 × 2 = 29–2 = 27

Третье число (3) – 27.

Вычислим четвертое число (4).

Для вычисления четвертого числа необходимо сложить цифры, из которых состоит третье число (3).

2 + 7 = 9

Четвертое число (4) – 9.

Если третье число однозначное, то четвертое число совпадает с ним, как если бы мы прибавили к третьему числу ноль.

Запишем полученные числа под датой рождения:

1 5 4 1 9 7 2

29 11 27 9

Впишем повторяющиеся цифры в психоматрицу (кроме цифры 0, которая в нее не входит)

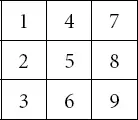
и получим запись цифровой матрицы, или психоматрицы, по конкретной дате рождения: 15 4 1972 (15 апреля 1972 года).