Александр Харчевников - Социальный метаболизм. Полилогический матричный анализ «обменных процессов» и стоимости

Предположим, в первом приближении, что структуры потребления каждого из агентов общественного воспроизводственного процесса равны между собой и равны структуре производства. При этом изначально в цикле этого воспроизводственного кругооборота обращения все агенты являются агентами-производителями, которые затем, с одной стороны, – выступают в качестве агентов-владельцев продуктов (матрица рис. 3), а позже, уже с другой стороны, – выступают на данном шаге «вторичного» распределения через «обмен» уже как агенты-потребители. (В данном случае структура производства и структура первого распределения равны между собой, ибо равны их матрицы (см. рис. 1 и 3), которые представляют натуральное выражение соответствующих структур в штуках).

Отобразим структуру производства в относительных единицах, имея ввиду, как исходную, натуральную количественную оценку в штуках каждого из производимых и полностью потребляемых j-ых продуктов. Соответствующая пропорция в потреблении каждым агентом-потребителем действительной жизни общества является пропорция, выраженная, например, в целых действительных числах или в долях от общего количества произведённых продуктов в штуках, которое по каждому j-ому продукту принимается за единицу (= 1,0).

Для рассматриваемого условного примера имеем следующую структурную пропорцию производства между j-ыми продуктами:

p 11: p 22: p 33= 6000: 9000: 12000 = 2: 3: 4.

Соответственно, для рассматриваемого условного примера, получим следующую пропорцию потребления в действительных числах между j-ыми продуктами по каждому агенту-потребителю, помня о её равенстве структуре производства:

2: 3: 4.

Соответственно в долях имеем следующую пропорцию потребления между i-ыми агентами по каждому j-ому продукту, помня, что эти доли для всех агентов одинаковы:

1/3: 1/3: 1/3,

при этом имеем по каждому j-ому продукту: 1/3 +1/3 +1/3 = 1,0.

Если отобразить эти доли (1/3: 1/3: 1/3) одновременно для всех j-ых продуктов и для каждого i-го агента как потребителя, то получим следующую матрицу, которая в форме таблицы дана на рисунке 4.

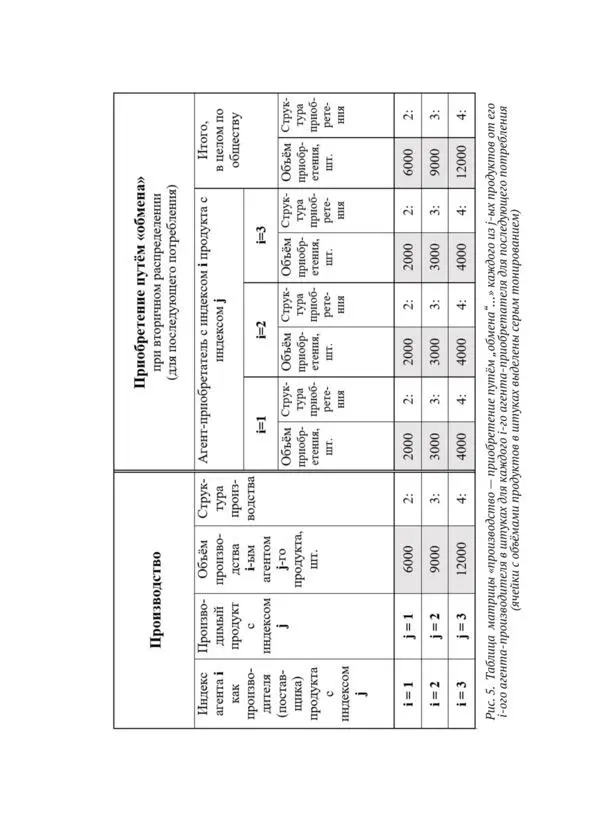
Тогда матрицу «обмена» производимыми в обществе j-ыми продуктами потребления между i-ыми агентами-производителями и i-ыми агентами-приобретателями (для последующего потребления уже как i-ыми агентами-потребителями) можно представить в форме таблицы рисунка 5. Этот «обмен» как элемент общественного метаболизма обеспечивает, с учётом последующего потребления, воспроизводственную жизнедеятельность i-ых агентов данного условного общества и вместе с этим, можно сказать, и само воспроизводство всей действительной жизни этого условного общества.

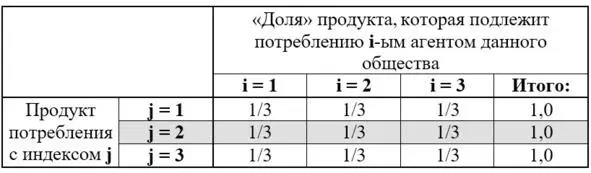
Рис. 4. Доли приобретения путём «обмена» каждого из j-ых продуктов от его объёма производства в штуках для каждого i-го агента как потребителя; в качестве примера здесь выделена строка одного из j-ых продуктов с индексом j = 2 и соответствующих долей его приобретения каждым из трёх i-ых агентов

Исходными данными для исчисления этой матрицы «обмена» являются матрица таблицы производства (см. рис. 1) и матрица долей приобретения путём «обмена» как «вторичного распределения» (см. рис. 4).

В качестве примера дадим следующий комментарий по строке агента-производителя продуктов с индексом i = 2,производящего продукт с индексом j = 2 в количестве 9000 штук (средняя строка матричной таблицы). Этот объём производства распределяется (можно сказать, – отчуждается), по 3000 штук между всеми тремя агентами-приобретателями. При этом агент с индексом i = 1 приобретает продукт с индексом j = 2 в объёме 3000 шт., агент с индексом i = 2 приобретает (сам у себя, то есть оставляет себе для собственного потребления) продукт с индексом j = 2 в количестве 3000 шт. и, наконец, агент с индексом i = 3 приобретает продукт с индексом j = 2 в количестве 3000 шт.

Пока лишь, предварительно, заметим, что фиксируемый в каждой ячейки матрицы объём того или иного продукта, с одной стороны, «отчуждается», а, с другой стороны, – «приобретается».

Четвёртый шаг – потребление.