Джесси Шелл - Геймдизайн [Как сознание определяет наше бытие] [litres]

Но это приводит нас к другому вопросу: сколько осмысленных выборов мы должны предоставить игроку? Майкл Матис указывает на то, что количество необходимых игроку вариантов зависит от количества его желаний.

• Если вариантов выбора > желаний, игрок ощущает их избыток.

• Если вариантов выбора < желаний, игрок расстраивается.

• Если варианты выбора = желаниям, игрок получает ощущение свободы и удовлетворенности.

Значит, чтобы правильно определить количество вариантов выбора, вам нужно рассчитать типы и количество действий, которые игроки захотят совершать. В некоторых ситуациях игроку нужно небольшое количество осмысленных вариантов выбора (выбирать между левым и правым поворотом на развилке будет интересно, но выбирать между 30 различными поворотами – это слишком). В другом случае огромное количество вариантов только на руку (например, интерфейс магазина одежды в The Sims ).

Осмысленные варианты выбора – это сердце интерактивности, поэтому следующая призма будет полезна всем без исключения.

Призма 39: Призма осмысленного выбора

Когда мы делаем осмысленный выбор, это позволяет нам ощутить значимость наших действий. Чтобы воспользоваться этой призмой, спросите себя:

• Перед каким выбором я ставлю игрока?

• Это осмысленный выбор? Почему?

• Я предоставляю игроку правильное количество вариантов выбора? Может ли большее количество вариантов выбора заставить игрока почувствовать больше власти? Если уменьшить их количество, станет ли игра более понятной?

• В моей игре присутствуют доминирующие стратегии?

Треугольность

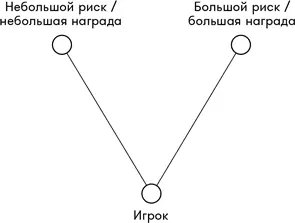
Один из самых интересных вариантов выбора, стоящих перед игроком, – перестраховываться и получить небольшую награду или серьезно рискнуть в надежде сорвать куш. Если игра правильно сбалансирована, подобные решения всегда даются очень тяжело. Я обнаружил, что когда ко мне приходят за помощью с прототипом игры, в которой «нет фана», в восьми из десяти случаев проблема заключается в отсутствии осмысленного выбора. Это иногда называют «риском асимметричного баланса», поскольку вы балансируете небольшие риски с небольшим вознаграждением вместе с большими рисками с большим вознаграждением, но такое название сложно произносить. Эти отношения возникают настолько часто и они настолько важны, что я придумал более удобное название: треугольность. Игрок – это один угол треугольника, выбор с небольшим риском – второй, а выбор с большим риском – третий.

Пример игры с правильно реализованной треугольностью – «Космические захватчики» ( Space Invaders) . Большую часть времени вы стреляете по «нижним» пришельцам возле своего корабля, зарабатывая за них 10, 20 и 30 очков. Они медлительны, поэтому в них легко попасть, а сбивая их, вы не даете им сбросить на себя бомбы. Однако периодически вверху экрана пролетает маленькая летающая тарелка красного цвета. Сама по себе она не несет угрозы, но попасть в нее трудно и опасно. Трудно потому, что тарелка летает очень далеко, а опасно потому, что для хорошего прицеливания вам нужно переключить внимание со своего корабля на нее, а это в разы увеличивает риск попадания в вас бомбы. Но если вы попадете, то получите от 100 до 300 очков! Без летающей тарелки «Космические захватчики» были бы слишком скучными – вам было бы не из чего выбирать, вы бы просто стреляли, стреляли и стреляли. Но с летающей тарелкой перед вами внезапно появляется сложный осмысленный выбор: сыграть осторожно или рискнуть ради большего количества очков? Треугольность настолько важна, что вам не обойтись без следующей призмы.

Призма 40: Призма треугольности

Предоставляя игроку выбор – сыграть осторожно и получить меньшую награду или рискнуть и попытаться получить больше, – вы делаете свою игру захватывающей и интересной. Чтобы воспользоваться Призмой треугольности, спросите себя:

• В моей игре присутствует треугольность? Если нет, как мне это исправить?

• Треугольность моей игры достаточно сбалансирована? Иными словами, соответствует ли награда риску?

Как только вы начнете анализировать игры на наличие треугольности, вы будете находить ее повсюду. Даже самая скучная и монотонная игра может быстро стать захватывающей, если добавить в нее немного треугольности.

Классический пример треугольности можно найти в книге Стивена Леви «Хакеры» (Hackers). Инженер из МТИ взламывает торговый автомат и изменяет принцип его работы: автомат предлагает человеку получить свою еду за обычную цену или рискнуть. Если человек выбирает риск, подбрасывается виртуальная монета, и он может либо заплатить за еду в два раза больше, либо получить ее бесплатно.