Анри Рухадзе - События и люди. Издание пятое, исправленное и дополненное.

была отнесена С. П. Дьяковым к области устойчивости плоских ударных волн относительно малых гофрировочных возмущений.

Последующие многочисленные исследования устойчивости плоских ударных волн [10–11], выполненные различными методами, не изменили границ области возникновения неустойчивости (8). Учет вязкости и теплопроводности газа [14, 15] также не изменили положение границ области (8). Однако уточнения нижней границы области (9), проведенные в работах {9-12, 16], показали, что

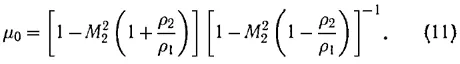
Дальнейший, более детальный анализ характера проведения малых возмущений показал, что в устойчивой области, если не учитывать вязкость и теплопроводность газа, возмущения ударной волны могут затухать во времени по степенному закону t -3/2 (возмущения в сильной ударной волне затухают по закону t -1/2 ). Учет конечной вязкости [13] или конечной проводимости среды за фронтом ударной волны, движущейся в поперечном магнитном поле, может приводить к экспоненциальному затуханию возмущений и к исчезновению области спонтанной генерации звука [19, 20].

В области (9) существования незатухающих (стационарных) гофрировочных возмущений фронта углам ориентации исходящих звуковых волн соответствует резонансное отражение звука фронтом ударной волны [22–25]. В этой области параметров задачи ударная волна, будучи нейтрально устойчивой к малым возмущениям, может оказаться неустойчивой к возмущениям конечной амплитуды, приводящим к расщеплению ударной волны на ударную волну меньшей интенсивности, контактный разрыв и длину разрежения [26–35]. Неустойчивость плоской ударной волны относительно одномерных возмущений тесно связана с эволюционностью поверхности разрыва — фронта ударной волны [22]. В дальнейшем было исследовано поведение малых возмущений на нелинейной стадии для неустойчивой ударной волны [25–35], когда на фронт волны подает конечное возмущение [27] и самопроизвольный распад [31, 32], приводящий для двумерных возмущений распад плоской волны на тройную конфигурацию — скачок [31]. Однако полного ответа на вопрос о характере явлений в неустойчивой области в настоящее время еще нет.

Проблема неустойчивости плоской ударной волны относительно двумерных возмущений тесно связана с тем, что двумерные возмущения могут обладать бесконечно большим коэффициентом роста

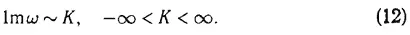
Учет конечной толщины фронта ударной волны — структуры волны, связанной с конечной вязкостью и (или) теплопроводностью, процессами химической кинетики, процессами ионизации, — может приводить к ограничению инкремента роста возмущений и нахождению возмущения, выживающего на нелинейной стадии. Можно предположить, что эволюция неустойчивой ударной волны и конечная стадия, в которую переходит неустойчивое состояние, тесно связаны с видом начальных возмущений — в зависимости от вида возмущений ударная волна может переходить в различные состояния.

Любопытная ситуация может существовать в области нейтральных колебаний даже в отсутствие химических реакций в зоне за фронтом волны, если рассматривать ее структуру. Нейтральноустойчивая ударная волна может генерировать турбулентность (при этом естественным образом возникает непрерывный спектр возмущений). Возникновение турбулентности может приводить не только к модификации коэффициентов переноса турбулентной вязкости и теплопроводности, но и изменять вид гидродинамических уравнений, описывающих поведение газа за фронтом волны: система осредненных уравнений Навье-Стокса, замыкающие уравнения для интенсивности турбулентных пульсаций. Поскольку в области нейтральных колебаний ударная волна неустойчива к возмущениям конечной амплитуды, возникновение турбулентных пульсаций выделяет интенсивность возмущений (порог), которые могут приводить к распаду волны на другие устойчивые конфигурации. Еще больший набор возможностей возникает для ударных волн в двухфазных средах и многокомпонентных плазмах, и здесь подходы, предложенные С. П. Дьяковым, могут оказаться весьма продуктивными.

— Но не только физиком-теоретиком от Бога был С. П. Дьяков. От Бога был его талант лектора. Ему не было 28 лет, когда он читал нам (Г. М. Арутюняну и А. А. Рухадзе), студентам 4-го и 5-го курсов физикотехнического факультета МГУ и факультета теоретической и экспериментальной физики МИФИ, спецкурс по нестационарным и нелинейным явлениям в гидродинамике. Во многом соответствующие главы «Механики сплошных сред» Л. Д. Ландау и Е. М. Лифшица напоминают содержание лекций С. П. Дьякова. А ведь книга эта тогда, когда он читал свои лекции в 1952 и 1953 гг., еще не была издана. А после издания всем, кто слушал спецкурс С. П. Дьякова, стало ясно, почему так часто его фамилия упоминается в этой книге. Книга Л. Д. Ландау и Е. М. Лифшица «Механика сплошных сред» вышла уже после гибели С. П. Дьякова.