Петр Путенихин - Силы притяжения, действующие на тело внутри диска

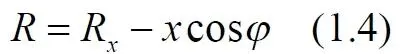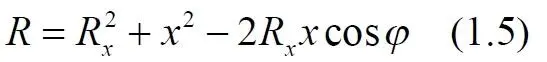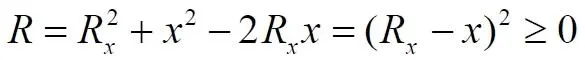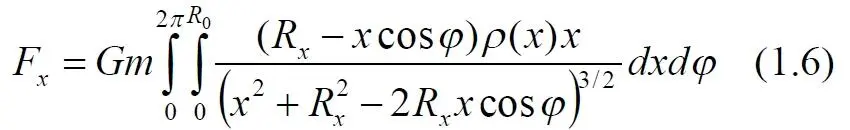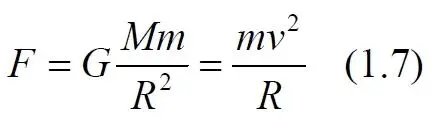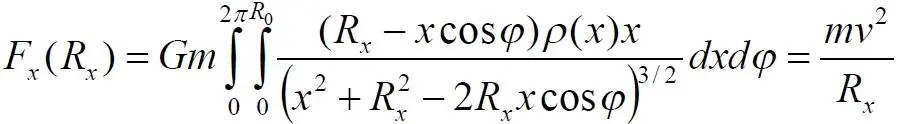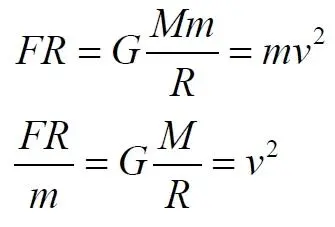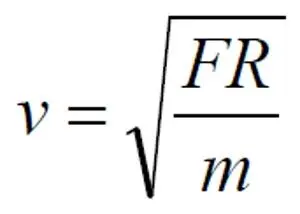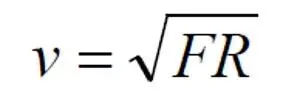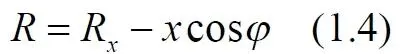
При вычислениях интеграла величина x для некоторого положения тела R x изменяется в интервале от 0 до R 0– на полном интервале радиуса диска. Этот интервал x следует формально разделить на два участка. На первом участке всегда x ≤ R x , на втором – всегда x > R x . Это приводит к тому, что в первом случае величина (1.4) и соответствующий ей интеграл в (1.3) оказывается положительной величиной всегда , а во втором, при некоторых углах φ, величина (1.4) и соответствующий ей интеграл в (1.3) становятся отрицательными. На знак интеграла знаменатель влияния не оказывает, поскольку сумма квадратов величин всегда больше их удвоенного произведения. Действительно, максимальное значение отрицательного слагаемого, способного сделать эту сумму отрицательной, определяется значением косинуса. Максимум отрицательной величины очевиден – это единичное значение косинуса:

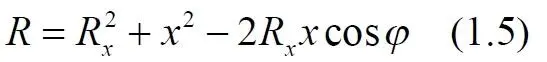
В этом случае получаем уравнение

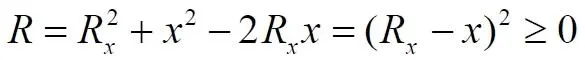
То есть, мы получили величину, которая никогда не принимает отрицательных значений, следовательно, и (1.5) также всегда положительна. Это означает, что при значениях параметра x , для некоторых обручей диска, являющихся для m внешними, сила притяжения при определённых углах φ имеет отрицательные значения, то есть, уменьшает силу притяжения тела в сторону центра диска. Запишем окончательное уравнение для результирующей силы, действующей на пробное тело m

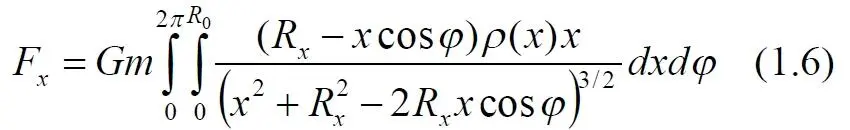
Выведенное интегральное уравнение позволяет построить кривую вращения по графику плотности вещества галактики. Для достижения поставленной цели, определения функции плотности по кривой вращения, нам, очевидно, нужна и функция этой кривой вращения.

Для большей наглядности в вычислениях мы будем использовать реальную кривую вращения – наблюдаемую кривая вращения галактики Млечный Путь. Функция этой кривой вращения представлена в табличном виде. Каждая кривая вращения является производной от силы притяжения и определяется из равенства этой силы силе центробежной

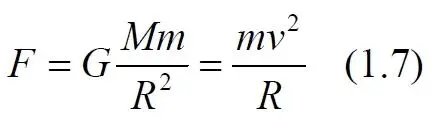
Силу притяжения нам позволяет вычислить наше интегральное уравнение (1.6), следовательно

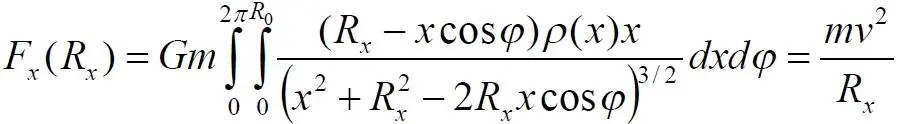
Преобразуем уравнение (1.7)

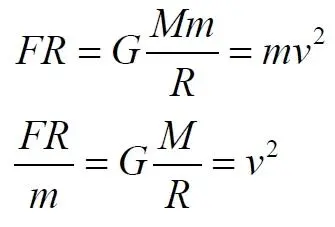
Поскольку известной, вычисляемой величиной у нас является сила F, среднюю часть уравнений отбрасываем

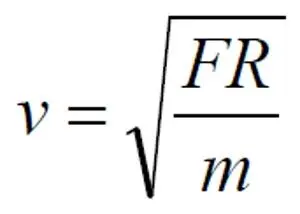
Здесь силой F является сила (1.6). Сделаем запись ещё короче, присвоив массе m единичное значение.

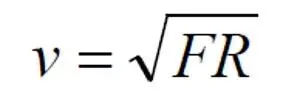
Это уравнение мы и будем использовать для построения кривой вращения, являющейся производной от функции плотности, поскольку сила F в уравнении (1.6) сама является функцией плотности. Заметим, что вывести обратную аналитическую зависимость – функции плотности от скорости вращения – задача, как оказалось, крайне сложная, если вообще разрешимая. Для решения поставленной задачи у нас, таким образом, остаётся только одно средство – итерация. Мы задаём некий закон, функцию плотности, по которой вычисляем кривую вращения, строим её график. Если этот график визуально, субъективно не совпадает с эталонным, корректируем функцию плотности и повторяем вычисления до тех пор, пока не будет достигнуто минимальное, приемлемое различие графиков.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.