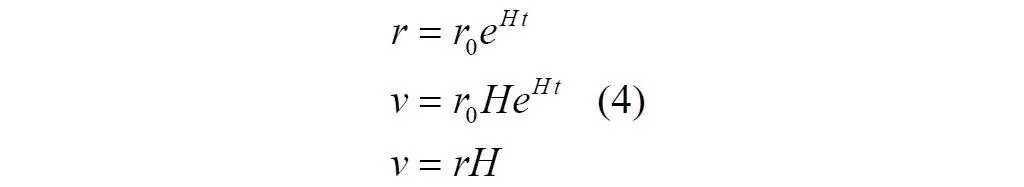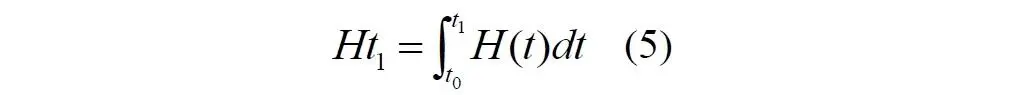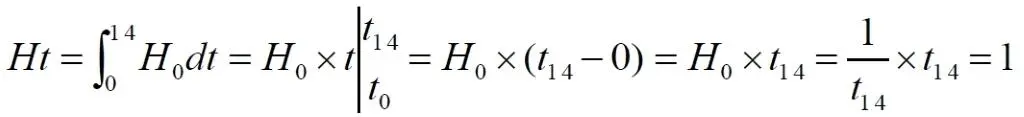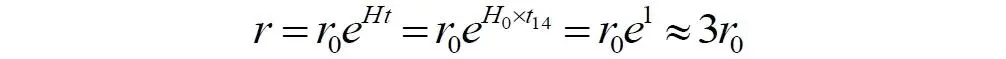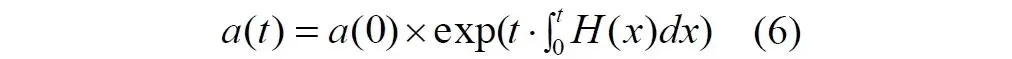Петр Путенихин - Уравнения движения в расширяющейся Вселенной

Таким образом, мы можем записать окончательно три уравнения: два уравнения движения для объекта, удаляющегося от наблюдателя в расширяющейся Вселенной: для удалённости и для скорости удаления, и закон Хаббла:

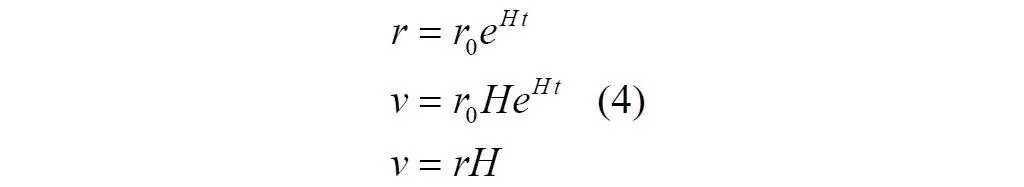
где:

H = H 0– параметр Хаббла, равный современному значению;

r 0– расстояние в момент начала расширения до объекта, удаляющегося от наблюдателя, либо расстояние между точкой пространства, где в будущем появится наблюдатель, Земля, и точкой пространства, где в будущем появится удаляющийся объекта – некоторая звезда, сверхновая.

Заметим, что решение уравнения (1) мы получили, исходя из неизменного, постоянного значения параметра H. Из этого же условия можно получить решение и в более общем, но несколько завуалированном виде для переменного значения параметра.

Для этого мы подменим величину Ht в экспоненте другой, интегральной величиной:

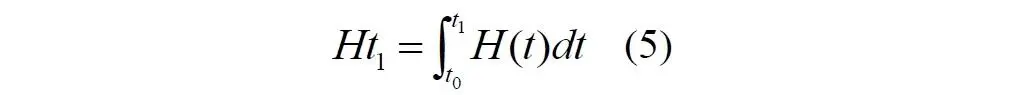
Правильность уравнения контролируем по размерности величин: слева и справа – они тождественно безразмерные. Величина t 1слева обязательно равна верхнему пределу интегрирования. Смысл интеграла состоит в том, что на каждом интервале времени dt новое расширение испытывает пространство, уже расширившееся на предыдущих этапах.

Математически здесь произведение Ht , как и раньше, является константой для наблюдаемого (!) момента (интервала) времени – t 1. Величина этой безразмерной константы определяется, по существу, интегральным значением реального параметра Хаббла, изменяющегося на интервале времени от начального t 0до конечного t 1. В частности, для всего времени существования Вселенной, то есть, принимая t 0 = 0, t 14 = 14, и современного постоянного значения параметра H 0 = 1/t 14, мы получим:

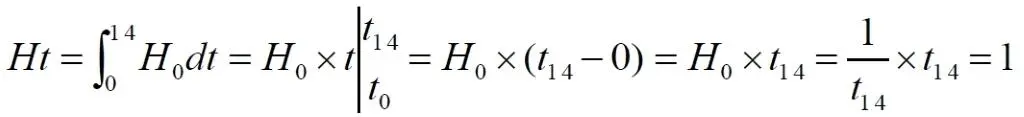
Подставляем в уравнение (3) и находим, что удалённость всех галактик во Вселенной за время её существования возросла примерно в 3 раза:

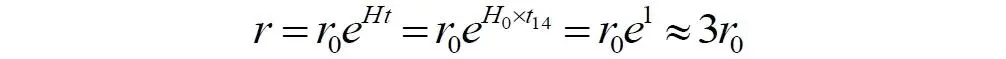
Это уравнение относится к любой единичной галактике во Вселенной. Например, галактика, находившаяся в начале расширения на удалении ~ 14 млрд. световых лет от Земли, сегодня находится на удалении ~ 42 млрд. световых лет.

Есть и ещё один подход к записи уравнения движения (4) (в терминах масштабного фактора):

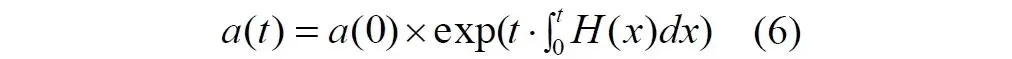
В этом случае параметр H ( x ) не является чётко выраженной функцией времени, а значение интеграла после его вычисления просто обозначается, именуется в дальнейшем как функция H ( t ) . Вид функции H ( t ) отличается от вида функции H ( x ) , именовать которую параметром Хаббла вряд ли уместно.

В космологии вместо реальных, физических скорости и удалённости используются соответствующие наблюдательные параметры – яркость удаленной галактики и её красное смещение. Яркость является математически тождественной величиной для удалённости. Определяя яркость стандартной свечи – сверхновой типа Ia, получают точное значение её удалённости. Чем ярче звезда, тем она ближе к нам. Второй параметр – красное смещение в точности соответствует скорости, с какой галактика удаляется от нас: чем больше смещение, тем выше скорость удаления. Иначе говоря, фактически в законе Хаббла присутствуют не скорости и расстояния, а красные смещения и яркости. Главным основанием для утверждений об ускоренном расширении Вселенной как раз и стал тот факт, что яркость дальних сверхновых типа Ia оказалась ниже, чем это должно следовать из закона Хаббла.

Следует отметить, что закон Хаббла, полученный в формализме общей теории относительности, может быть выведен и средствами физики Ньютона. В интернете и в литературе нередко приводится условная иллюстрация расширения пространства на примере резинового шара с наклеенными на него монетками-галактиками. Раздувание шара приводит к тому, что расстояние между монетами возрастает, причём каждая из них может считать себя центром, от которого удаляются все остальные.