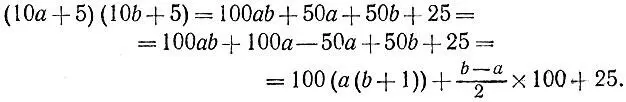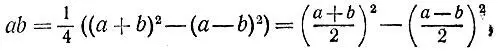Сергей Гашков - Примени математику

179*2,5 = 1790:4 = 447,5, 179*1,25 = 179 + 179:4 = 179 + 44,75 = 1790:8 = 223,75, 179*1,5 = 179 + 179:2 = 179 + 89,5 = 268,5, 179*0,75 = 179 - 179:4 = 179 - 44,75 = 134,25.Наконец, умножение на 15 и на 75 можно представить соответственно как умножение на 1,5 и на 0,75 с последующим умножением соответственно на 10 и на 100, например

34*15 = (34 + 17)10 = 510, 34*75 = (34 - 8,5)100 = 2550. 1.11.При последовательном умножении числа на возрастающие степени двойки, т. е. при последовательном удвоении, можно фиксировать те числа, сумма или разность которых дает искомое произведение. Так, умножение числа 139 на 14 = 2 4- 2 1 можно провести следующим образом:

139*14 = 139*2 4- 139*2 1= 2224 - 278 = 1946(здесь, разумеется, использованы выкладки, приведенные в условии задачи). Аналогично умножение на 35 = 2 6+ 2 1+ 2 0 можно провести так:

139*35 = 139*2 6+ 139*2 1- 139*2 0= 4448 + 278 + 139 = 4865. 1.12.Деление на степень двойки можно провести в такой же последовательности, как умножение, описанное в формулировке задачи 1.11, но, естественно, с заменой операции умножения операцией деления, например,

139:32 = 69,5:16 = 34,75:8 = 17,375:4 = 8,6875:2 = 4,34375. 1.13.Пусть надо перемножить два числа вида 1a -и 1b -. Тогда имеем равенства

(10+а)(10+b) = 100 + 10а + 10b + ab = 10(а+b) + 100 + ab,которые подтверждают правильность предложенного в условии задачи способа.

1.14.Из равенства

(100-а) (100-b) = (100-а)100 - 100b + ab = 100 ((100-a)-b) + ab,где а и b - дополнения первого и второго сомножителя до 100 соответственно, вытекает правильность предложенного способа.

1.15.Ответ получен из верного равенства

(1000-а) (1000-b) = (1000-а)1000 - 1000b + ab = 1000 ((1000-a) - b) + abпри а = 13 и b = 4. Таким образом, для перемножения двух трехзначных чисел, близких к 1000, достаточно вычесть из одного числа дополнение второго до 1000 и, увеличив разность в 1000 раз, прибавить к ней произведение дополнений исходных чисел до 1000.

1.16.Пусть нужно перемножить числа 10а+b и 10а+с , удовлетворяющие условию b+с = 10. Тогда имеем

b>(10а+b)(10а+с) = 100а 2+ 10aс + 10bа + bс = 100а 2+ 10а(b+с) + bс = 100а 2+ 100а + bс = 100а(а+1) + bc, что и требовалось доказать.

1.17.Для возведения в квадрат числа, оканчивающегося на 5, достаточно отбросить у него последнюю цифру, а затем перемножить полученное число с числом, большим его на 1, и приписать к результату справа 25. Это правило является следствием равенства, доказанного в решении задачи 1.16, если в нем положить b = с = 5.

1.18.Пусть перемножаются числа 10а+5 и 106+5. Правильность предложенного способа вытекает из следующих равенств:

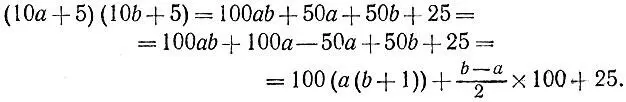
1.19.Произведение чисел а и b можно найти по формуле

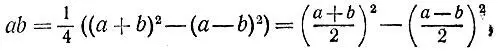
удобной для применения в случае одновременной четности или одновременной нечетности сомножителей (в противном случае их полусумма и полуразность были бы нецелыми) и в случае, когда эти сомножители близки друг к другу.

1.20.Квадраты двух соседних чисел различаются на сумму этих чисел, поскольку имеют место равенства

(а+1) 2- а 2= 2а + 1 = (а+1) + а.Аналогично, если числа различаются на 2, то разность их квадратов

(a+2) 2- а 2= 4а + 4 = 4(а+1) = 2((а+2) + а)равна удвоенной сумме этих чисел. Так как любое целое число отличается от ближайшего числа, кратного 5, не более чем на 2, то, пользуясь указанными здесь соображениями, можно восстановить его квадрат, например,

31 2= 30 2+ (31 +30) = 900 + 61 = 961, 32 2= 30 2+ 2 (32 + 30) = 900 + 124 = 1024, 33 2= 35 2- 2 (33+ 35) = 1225 - 136 = 1089, 34 2= 35 2- (34 + 35) = 1225 - 69 = 1156. 1.21.Кубы двух соседних чисел а и а+1 различаются на число

(а+1) 3- а 3= 3а 2+ 3а + 1 = 3а(а+1) + 1,равное утроенному произведению этих чисел, увеличенному на 1. Поэтому, зная куб, скажем, числа 30, мы быстро находим куб следующего числа:

31 3= 30 3+ 3*30*31 + 1 = 27 000 + 2790 + 1 = 29 791. 1.22.Вычисление квадратов в разобранных примерах основано на формуле

a 2= (а+b)(а-b) + b 2,в которой удачный подбор числа b сильно облегчает выкладки: во-первых, один из сомножителей должен оказаться "круглым" числом (желательно, чтобы ненулевой его цифрой была только первая), во-вторых, само число b должно легко возводиться в квадрат, т. е. должно быть небольшим. Эти условия реализуются как раз на числах а, близких к "круглым".

1.23.Пусть надо найти квадрат числа а, заключенного между 25 и 50. Тогда, пользуясь формулой из решения задачи 1.22, получаем