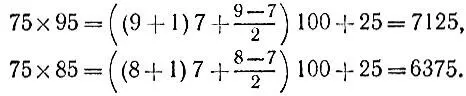Сергей Гашков - Примени математику

1.15. Умножение чисел, близких к 1000При перемножении чисел 987 и 996 были проделаны вычисления:

987*996 = (987-4)1000 + 4*13 = 983 052.Убедитесь, что в результате найден верный ответ, и объясните способ его получения (сравните с задачей 1.14).

1.16. Устное умножениеДокажите, что для перемножения двух чисел, у которых цифры единиц в сумме дают 10, а цифры других разрядов совпадают, достаточно число, получающееся в результате отбрасывания цифры единиц, умножить на следующее за ним натуральное число и, увеличив произведение в 100 раз, прибавить к нему произведение цифр единиц исходных чисел. Например, верны выкладки

62*68 = 6*7*100 + 2*8 = 4216. 1.17. Квадрат числа, оканчивающегося на 5Сформулируйте общее правило, с помощью которого возведены в квадрат следующие числа:

85 2= 8*9*100 + 25 = 7225, 115 2= 11*12*100 + 25= 13225.Откуда вытекает справедливость этого правила?

1.18. Если числа оканчиваются на 5Докажите, что для перемножения двух чисел, оканчивающихся на 5, достаточно отбросить у каждого числа последнюю цифру, а затем, увеличив большее из полученных чисел на 1, умножить его на меньшее из них и прибавить к результату полуразность тех же чисел, наконец, увеличить ответ в 100 раз и прибавить 25. Например, пользуясь указанным способом, находим произведения

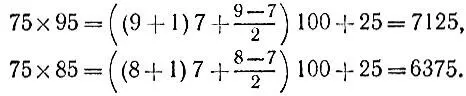
1.19. С помощью квадратовЕсли вы хорошо помните или умеете быстро восстанавливать в памяти квадраты натуральных чисел, то вы сможете и быстро перемножить, скажем, числа 32 и 36 следующим способом:

32*36 = 34 2- 2 2= 1156 - 4 = 1152.Обоснуйте верность приведенных выкладок и подумайте, к каким парам чисел удобнее применять указанный способ перемножения

чисел.

1.20. Квадраты близких чиселПусть вы помните квадрат какого-то числа и хотите по нему быстро восстановить квадрат числа, отличающегося от исходного на 1 или 2. Как это можно сделать, не производя операции возведения в квадрат?

Если вы помните только квадраты чисел, кратных 5, то без особого напряжения сможете восстанавливать квадраты остальных целых чисел. Как именно?

1.21. Следующий кубПусть вам известен куб некоторого числа. Как с его помощью проще найти куб следующего числа?

1.22. Квадрат числа, близкого к "круглому"Быстрому возведению в квадрат может способствовать умение перемножать в уме любые числа с некоторыми числами специального вида, например

192 2= 200*184 + 8 2= 36 864, 412 2= 400*424 + 12 2= 169 744.На каком приеме основаны вычисления квадратов в данных примерах?

1.23. Следующие 25 квадратовЕсли вы знаете квадраты всех чисел от 1 до 25, то вам нет никакой необходимости заучивать квадраты следующих 25 чисел. Для возведения в квадрат любого числа, заключенного между 25 и 50, достаточно отнять от него 25 и, увеличив результат в 100 раз, прибавить к нему квадрат дополнения этого числа до 50. Например, справедливы равенства

37 2= (37-25)100 + (50-37) 2= 1200 + 169 = 1369.Дайте обоснование предложенному способу.

1.24. Квадраты чисел, больших 50Как изменить описанную в задаче 1.23 процедуру возведения в квадрат, чтобы она годилась и для двузначных чисел, больших 50?

1.25. Квадраты чисел, близких к 500При возведении в квадрат числа 492 были проделаны вычисления

492 2= (492-250)1000 + (500-492) 2= 242 064.Убедитесь, что в результате найден верный ответ, и сформулируйте общее правило возведения в квадрат чисел, близких к 500 (сравните с задачами 1.23 и 1.24).

1.1.Имеет смысл сосчитать, сколько раз среди слагаемых встречаются в отдельной части числа 1, 2, 3, ..., 9. Если количества этих чисел скажутся соответственно равными n 1, n 2, n 3, ..., n 9, то искомая сумма будет равна 1*n 1+ 2*n 2+ 3*n 3+ ... + 9*n 9и подсчет этой суммы можно будет произвести более экономно, а значит, с меньшей вероятностью ошибки.

1.2.Если чисел достаточно много, то среди них с большой вероятностью найдутся пары или тройки чисел, дающие в сумме целое число-десятков. Заменим такие группы чисел их суммами, а затем среди новых слагаемых выделим аналогично группы чисел, дающие в сумме целое число сотен. Действуя таким образом, мы сильно упростим работу по сложению исходных чисел. Например, складывая числа 17, 96, 72, 29, 93, 32, 87, 68, 84, 37, 13, 92, 55, 61, 45, 34, 73, 29, 20, 64, получаем