2.5. Упрощение для 4Согласно общему признаку делимости на 2 k, чтобы узнать, делится ли данное число на 4, достаточно проверить, делится ли на 4 число, полученное из данного отбрасыванием всех его цифр, кроме двух последних.
Как можно упростить проверку делимости двузначного числа на 4?
2.6. Упрощение для 8Согласно общему признаку делимости на 2к, чтобы узнать, делится ли данное число на 8, достаточно проверить, делится ли на 8 число, полученное из данного отбрасыванием всех его цифр, кроме трех последних.
Как можно упростить проверку делимости трехзначного числа на 8?
2.7. По сумме цифрДокажите, что любое число при делении как на 3, так и на 9 дает тот же остаток, что и сумма его цифр.
2.8. Упрощение для 3Согласно утверждению задачи 2.7, данное число делится на 3 в том и только в том случае, если на 3 делится сумма его цифр.
Как можно упростить проверку делимости суммы цифр числа на 3, не находя самой этой суммы?
2.9. Упрощение для 9Согласно утверждению задачи 2.7, данное число делится на 9 в том и только в том случае, если на 9 делится сумма его цифр.
Как можно упростить проверку делимости суммы цифр числа на 9, не находя самой этой суммы?
2.10. Только 3 и 9Докажите, что если признак делимости на число m (большее 1) не зависит от порядка цифр делимого, то само число m может быть равно только 3 или 9.
2.11. Проверка сложенияВы сложили несколько чисел и хотите проверить правильность своих вычислений. Для этого можно поступить следующим образом: найти остаток от деления на 9 суммы цифр полученного ответа, затем найти остаток от деления на 9 общей суммы цифр всех слагаемых. Если указанные два остатка не совпадут, то в вычислениях имеется ошибка. Дайте объяснение предложенному способу проверки сложения.
Придумайте аналогичный способ проверки вычисления алгебраической суммы, т. е. суммы нескольких целых чисел разных знаков.
2.12. Проверка умноженияВы перемножили несколько чисел и хотите проверить правильность своих вычислений. Для этого можно поступить следующим образом: найти остаток от деления на 9 суммы цифр полученного ответа, затем перемножить остатки от деления на 9 суммы цифр каждого из сомножителей и найти остаток от деления на 9 этого произведения, Если указанные два остатка не совпадут, то в вычислениях имеется ошибка.
Дайте объяснение предложенному способу проверки умножения. Придумайте аналогичный способ проверки деления (возможно, с остатком).
2.13. Надежна ли проверка?В задачах 2.11 и 2.12 приведены способы проверки вычислений, которые позволяют усомниться в правильности произведенных выкладок в случае несовпадения некоторых остатков от деления на 9.
Можно ли утверждать, что если указанные остатки совпали, то вычисления не содержат ошибок?
Можно ли это утверждать при условии, что вы ручаетесь за правильность всех цифр полученного в ответе числа, кроме, быть может, одной цифры?
2.14. В магазинеВы пришли в магазин и хотите купить 8 одинаковых авторучек, несколько карандашей по 4 копейки, линейку за 9 копеек, 2 общие тетради по 18 копеек и 12 тонких тетрадей. Продавец подсчитал общую стоимость товаров и попросил вас уплатить в кассу 5 рублей 27 копеек.
Как, по-вашему, не ошибся ли продавец?
2.15. Разложив на множителиСформулируйте признаки делимости на 6, 12, 15, 18, 24, 36, 45. Достаточно ли для проверки делимости числа на 24 установить его одновременную делимость на 4 и на 6?
2.16. Признак ПаскаляДля получения признака делимости на m найдем заранее остатки m 1, m 2, m 3,... от деления на m чисел 10 1, 10 2, 10 3,..., соответственно. Для любого числа 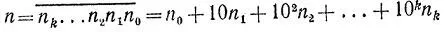 определим число
определим число
f m(n)= n 0+m 1n 1+m 2n 2+. ..+m kn k .
Докажите, что числа n и f m(n) дают одинаковые остатки при делении на m и могут делиться на m только одновременно. Проверьте, что нахождение остатка m k+1при k = 1, 2, 3,... можно осуществить проще, если заметить, что он равен остатку от деления на m числа 10m k, (вместо числа 10 k+1).
2.17. Частные случаиПроверьте, что сформулированные выше признаки делимости на 2, 3, 5 и 9 (см. задачи 2.4, 2.8, 2.1 и 2.9) представляют собой частные случаи признака Паскаля.
2.18. Что лучше?Получите из признака Паскаля признаки делимости на 4 и на 8. Сравните их с предложенными ранее в задачах 2.5 и 2.6.
2.19. Модификация признака ПаскаляДля практического применения признака делимости на m, сформулированного в задаче 2.16, бывает удобнее некоторые из остатков m 1, m 2, m 3,... от деления на m чисел 10 1, 10 2, 10 3,..., Заменить соответствующими недостатками (особенный аффект от такой замены достигается в тех случаях когда недостатки близки к нулю).
Читать дальше

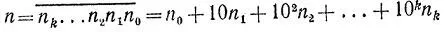 определим число
определим число









