Марина Васильева - Инженерная графика

Для выполнения этих построений целесообразно выбирать рациональный способ выполнения чертежа. Выбор рационального способа решения задачи сокращает время, затрачиваемое на работу. Например, при построении равностороннего треугольника, вписанного в окружность, более рационален способ, при котором построение выполняют рейсшиной и угольником с углом 60° без предварительного определения вершин треугольника (см. рисунок 2а,б).

Менее рационален способ решения той же задачи с помощью циркуля и рейсшины с предварительным определением вершин треугольника (см. рисунок 2, в).

Деление окружности на три равные части. Устанавливают угольник с углами 30 и 60° большим катетом параллельно одной из центровых линий. Вдоль гипотенузы из точки 1 (первое деление) проводят хорду (рисунок 2,а), получая второе деление – точку 2 . Перевернув угольник и проведя вторую хорду, получают третье деление – точку 3 (рисунок 2,б). Соединив точки 2 и 3 и 3 и 1 прямыми линиями, получают равносторонний треугольник.

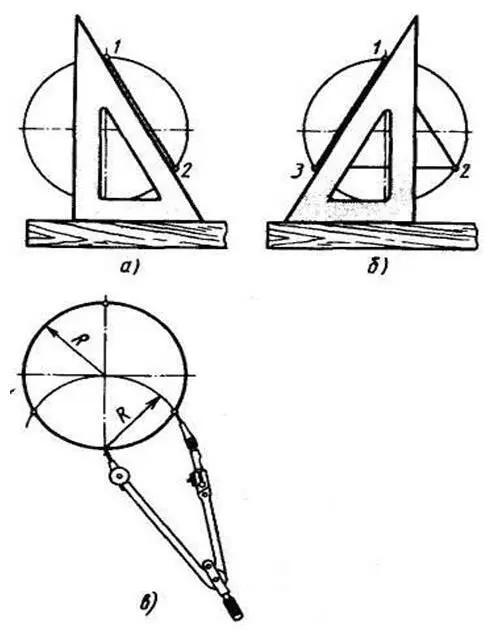
Рисунок 2 – Деление окружности на три равные части: а, б – с помощью угольника, в – с помощью циркуля

Ту же задачу можно решить с помощью циркуля. Поставив опорную ножку циркуля в нижний или верхний конец диаметра (рисунок 2, в), описывают дугу, радиус которой равен радиусу окружности. Получают первое и второе деления. Третье деление находится на противоположном конце диаметра.

Деление окружности на шесть равных частей . Раствор циркуля устанавливают равным радиусу R окружности. Из концов одного из диаметров окружности (из точек 1, 4 ) описывают дуги (рисунок 3 а, б). Точки 1, 2, 3, 4, 5, 6 делят окружность на шесть равных частей. Соединив их прямыми линиями, получают правильный шестиугольник (рисунок 3, б).

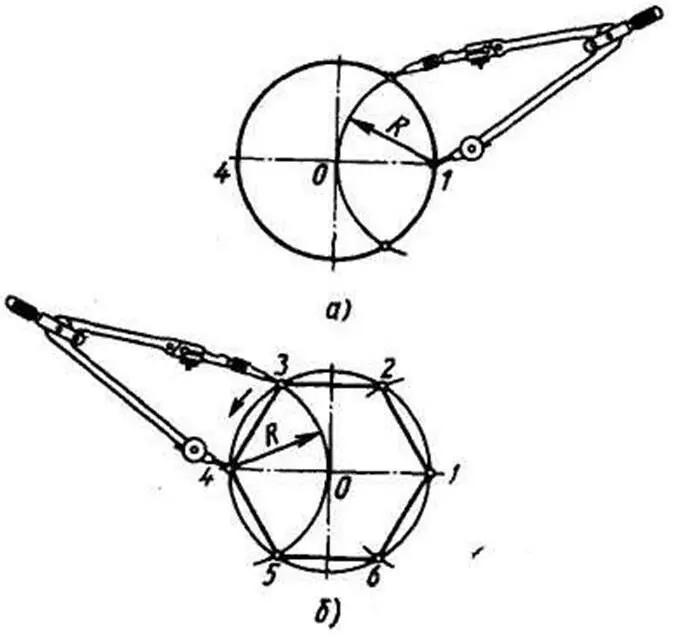
Рисунок 3 – Деление окружности на шесть равных частей с помощью циркуля

Ту же задачу можно выполнить с помощью линейки и угольника с углами 30 и 60° (рисунок 4). Гипотенуза угольника при этом должна проходить через центр окружности.

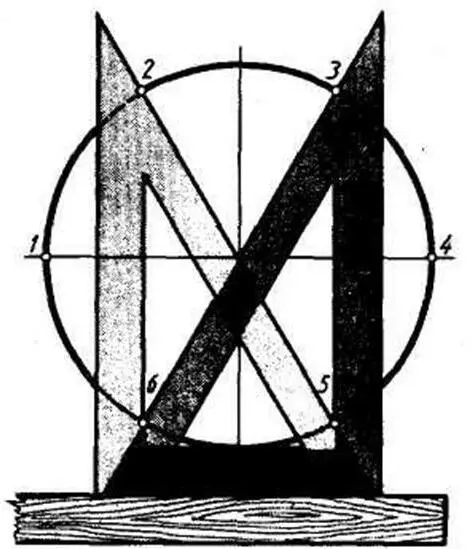
Рисунок 4 – Деление окружности на шесть равных частей с помощью угольника

Деление окружности на восемь равных частей . Точки 1, 3, 5, 7 лежат на пересечении центровых линий с окружностью (рисунок 5). Еще четыре точки находят с помощью угольника с углами 45°. При получении точек 2, 4, 6, 8 гипотенуза угольника проходит через центр окружности.

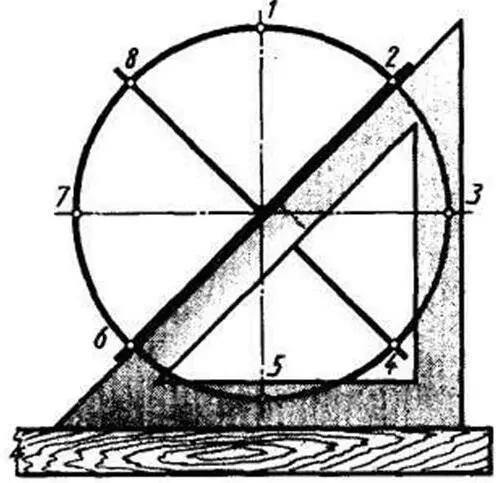
Рисунок 5 – Деление окружности на восемь равных частей с помощью угольника

Деление окружности на любое число равных частей . Для деления окружности на любое число равных частей пользуются коэффициентами, приведенными в таблице 1.

Длину l хорды, которую откладывают на заданной окружности, определяют по формуле:

где l – длина хорды;

d – диаметр заданной окружности;

k – коэффициент, определяемый по таблице 1.

Чтобы разделить окружность заданного диаметра 90 мм, например, на 14 частей, поступают следующим образом.

Таблица 1 – Коэффициенты для деления окружности

В первой графе таблицы 1 находят число делений n , т.е. 14. Из второй графы выписывают коэффициент k , соответствующий числу делений n . В данном случае он равен 0,22252. Диаметр заданной окружности умножают на коэффициент и получают длину хорды:

Полученную длину хорды откладывают циркулем-измерителем 14 раз на заданной окружности.

Нахождение центра дуги и определение величины радиуса . Задана дуга окружности, центр и радиус которой неизвестны.

Для их определения нужно провести две непараллельные хорды (рисунок 6,а) и восставить перпендикуляры к серединам хорд (рисунок 6,б). Центр О дуги находится на пересечении этих перпендикуляров.