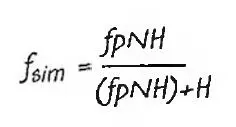Тед Косматка - Потрепващите

Тя взе една книга от купчината хартии. Беше голяма и тежка. Подхвърли ми я.

Аз я улових, видях в нея отметка и отворих отбелязаната страница.

Не беше, каквото очаквах.

— Ренесансово изкуство?

На страницата имаше изображение на архангел Гавраил, който надува своята тръба и всички ангели от небесата се бяха събрали в кръг около него, който продължаваше в далечината. Имаше нещо фрактално и красиво в обръча от крила — като скрита в модела мандала.

— Тръбата на Гавраил — каза тя. — Той ще я надуе в деня на Страшния съд, когато всички ще отговаряме за греховете си. — Обърна се да погледне пак в книгата. — Винаги съм харесвала тази картина. Тръбата и ангелите. Но има и още една.

Тя взе от масата книга с оръфани краища. Тази беше за математика. Викърс я сложи на масата пред мен и разлисти страниците.

— Това също е тръбата на Гавраил — каза тя. — Парадокс.

Приближих се и погледнах над рамото й. На страницата имаше графика на ƒ: х като функция на 1/х.

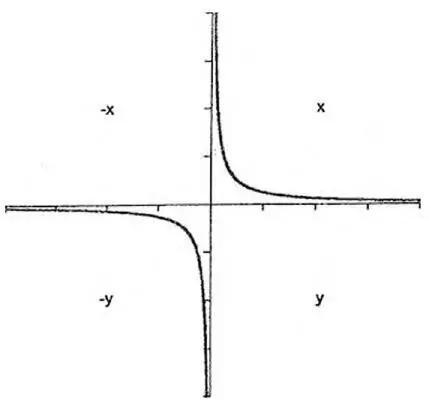
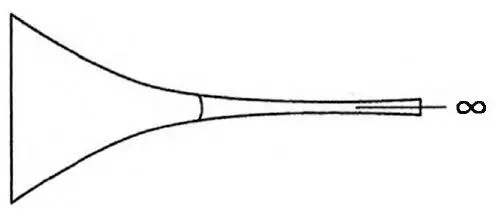
— Реципрочното на хикс, завъртане около собствената ос — каза Викърс. — Обект, който е по-голям отвътре, отколкото отвън.

— Математическо чудовище — казах аз, познавах добре тази фигура. — Графиката няма край. Тръбата на Гавраил е бездънна. Нарича се още Тръба на Торичели. Краен обем, но безкрайна повърхнина.

— Това е метафора за Вселената. Нещо, за което Еванджелиста Торичели никога не би се досетил, когато е описвал тази фигура през седемнайсети век.

— Защо да е метафора?

— Вселената не е сфера; тя е фуния. Макар че и това описание не е съвсем вярно, нали? Метафора за метафора, която не пасва съвсем.

Взирах се в нея. Сякаш слушах лекция за струнната теория. Дори не беше погрешно, а просто нечия идея как би могло да бъде.

— Просто думи — казах аз малко по-рязко от необходимото.

Това ми напомни за историите на мама — неща, които нямаха никаква пресечна точка с реалността.

— Думи — съгласи се Викърс. — И данни. Ето ви още една метафора, ако така искате. Чували ли сте за Вселената матрьошка?

— Руските кукли ли имате предвид? — Това беше космологична теория, която се пробутваше през последните десетилетия от някои от най-спекулативните мислители. — Идеята, че вселените може да са напъхани една в друга.

Тя кимна.

— Същият принцип като при Тръбата на Торичели. Краен обем, но безкрайна повърхнина — Тръбата на Гавраил в по-голям мащаб. Като нашата Вселена е само една от цяла каскада вселени, вместени една в друга. Но помислете за уникалната перспектива на човечеството.

— Например?

— Коя е човешката ниша във всичко това? Защо хората са различни? Заради нашата способност да наблюдаваме и да отразяваме онова, което наблюдаваме. Нашата способност да моделираме света около нас. Първо в картини и книги, а сега и чрез технологии, моделите стават все по-сложни.

Спомних си за пещерните рисунки, които Брайтън спомена.

— Това е импулс на нашата природа — продължи тя. — Първо виждаме, после отразяваме. Представете си картина на велосипед; после си представете велосипеда, изобразен като скулптура. Накрая си представете толкова съвършена скулптура, до най-малката подробност, че е напълно неразличима от онова, което отразява. Представете си, че можете да подкарате тази съвършена скулптура. Нима всъщност това не е пак велосипед? С напредъка на цивилизацията и с усъвършенстването на способността ни да възпроизвеждаме Вселената, кога достигаме онзи момент, в който моделът става онова, което отразява? Ами ако вътре в този безкрайно сложен модел се зароди цивилизация, която от своя страна ще породи собствен модел?

— Модел ли? — попитах. — За конструиране на реалност ли говорите?

— Всички реалности са конструирани по един или друг начин, нали? Или чрез нечий труд и воля, или се появяват като самовъзникващи от основните закони на една система. Ник Бостром, учен от Оксфорд, е пресметнал вероятността да се намираме в подобна възникнала в друга система.

Викърс дръпна разделителя от книгата и го разгъна — намачкан лист хартия, на който бяха изписани числа и букви. Тя го приглади на масата и рече:

— Ето неговата формула.

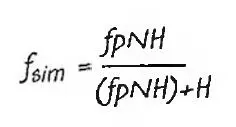
— В подобна каскада може да има безкраен брой вселени. Съществуването не е циклично, а серийно.