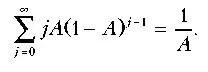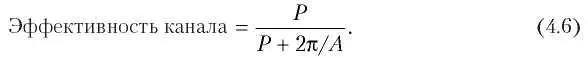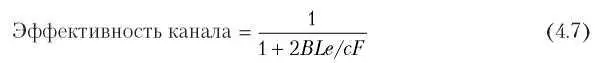При третьем столкновении (вероятность такого события после двойного столкновения равна 1/4) интервалы будут выбираться в диапазоне от 0 до 2 3- 1.
В общем случае, после i столкновений случайный номер выбирается в диапазоне от 0 до 2 i- 1, и это количество интервалов станция пропускает. Однако после 10 столкновений подряд интервал рандомизации фиксируется на отметке 1023. После 16 столкновений подряд контроллер признает свое поражение и возвращает компьютеру ошибку. Дальнейшим восстановлением занимаются более высокие уровни.
Этот алгоритм, называемый экспоненциальным двоичным алгоритмом выдержки( binary exponential backoff), был выбран для динамического учета количества станций, пытающихся осуществить передачу. Если выбрать интервал рандомизации равным 1023, то вероятность повторного столкновения будет пренебрежимо мала, однако среднее время ожидания составит сотни тактов, в результате чего среднее время задержки будет слишком велико. С другой стороны, если каждая станция будет выбирать время ожидания всего из двух вариантов, 0 и 1, то в случае столкновения сотни станций они будут продолжать сталкиваться снова и снова до тех пор, пока 99 из них не выберут 1, а одна станция — 0. Такого события можно будет ждать годами. Экспоненциально увеличивая интервал рандомизации по мере возникновения повторных столкновений, алгоритм обеспечивает небольшое время задержки при столкновении небольшого количества станций и одновременно гарантирует, что при столкновении большого числа станций конфликт будет разрешен за разумное время.
Если коллизии не произошло, отправитель предполагает, что кадр, вероятно, был успешно доставлен. Таким образом, ни в CSMA/CD, ни в Ethernet подтверждения не применяются. Такой вариант подходит для кабельных и оптоволоконных каналов с низким числом ошибок. Любые возникающие ошибки распознаются с помощью кода CRC и исправляются более высокими уровнями. Как мы увидим далее, в зашумленных беспроводных каналах подтверждения используются.
4.3.3. Производительность сети Ethernet
Оценим производительность классической сети Ethernet в условиях большой постоянной загрузки, то есть когда k станций постоянно готовы к передаче. Строгий анализ экспоненциального двоичного алгоритма выдержки довольно сложен. Вместо этого мы последуем за рассуждениями Меткальфа (Metcalfe) и Боггса (Boggs) (1976) и предположим, что вероятность повторной передачи в каждом интервале времени постоянна. Если каждая станция передает в течение одного интервала времени с вероятностью р, то вероятность того, что какой-либо станции удастся завладеть каналом, равна

Значение A будет максимальным, когда р = 1/k. При k, стремящемся к бесконечности, A будет стремиться к 1/e. Вероятность того, что период соревнования за канал будет состоять ровно из j интервалов, будет равна A(1 - A) j-1, следовательно, среднее число интервалов борьбы за канал будет равно
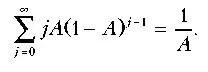
Так как длительность каждого интервала времени равна 2т, средняя продолжительность периода борьбы будет составлять w = 2т/А При оптимальном значении вероятности p среднее количество интервалов за период борьбы никогда не будет превосходить е, таким образом, средняя продолжительность периода борьбы будет равна 2те « 5,4т.
Если среднее время передачи кадра составляет P с, то эффективность канала при его сильной загруженности будет равна:
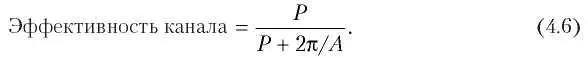
В этой формуле мы видим, как максимальная длина кабеля влияет на производительность. Чем длиннее кабель, тем более долгим становится период борьбы за канал. Из этих рассуждений становится понятно, почему стандарт Ethernet накладывает ограничение на максимальное расстояние между станциями.
Полезно переформулировать выражение (4.6) в терминах длины кадра F, пропускной способности сети B, длины кабеля L и скорости распространения сигнала c для оптимального случая: e интервалов столкновений на кадр. При P = F/B выражение (4.6) примет вид:
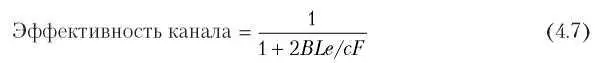
Читать дальше
Конец ознакомительного отрывка
Купить книгу