4.1.1. Статическое распределение канала
Традиционный способ разделения одного канала, например телефонного кабеля, между многочисленными конкурирующими пользователями — в разделении емкости с помощью одной из схем мультиплексирования или уплотнения каналов, таких как FDM( Frequency Division Multiplexing — частотное уплотнение). При наличии N пользователей полоса пропускания делится на N диапазонов одинаковой ширины, и каждому пользователю предоставляется один из них. Поскольку при такой схеме у каждого оказывается свой личный частотный диапазон, то конфликта между пользователями не возникает. При постоянном небольшом количестве абонентов, каждый из которых отправляет стабильный поток или большие партии трафика, частотное уплотнение предоставляет простой и эффективный механизм распределения. Аналогичный беспроводной пример — радиостанции FM-диапазона. Каждая станция получает часть FM-полосы и использует ее почти постоянно, передавая свой сигнал.
Однако при большом и постоянно меняющемся количестве отправителей данных, или пульсирующем трафике, частотное уплотнение не может обеспечить достаточно эффективное распределение канала. Если количество пользователей в какой-либо момент времени меньше числа диапазонов, на которые разделен спектр частот, то большая часть спектра не используется и тратится попусту. Если, наоборот, количество пользователей окажется больше числа доступных диапазонов, то некоторым придется отказать в доступе к каналу, даже если абоненты, уже захватившие его, почти не будут использовать пропускную способность.
Даже если предположить, что количество пользователей можно каким-то способом удерживать на постоянном уровне, то разделение канала на статические подканалы все равно является неэффективным. Основная проблема здесь состоит в том, что
если какая-то часть пользователей не пользуется каналом, то эта часть спектра просто пропадает. Они сами при этом занимают линию, не передавая ничего, и другим не дают передать данные. Статическое разделение плохо подходит для большинства компьютерных систем, в которых трафик является чрезвычайно неравномерным, с частыми пиками (вполне обычным является отношение пикового трафика к среднему как 1000:1). Следовательно, большую часть времени большая часть каналов не будет использоваться.
То, что характеристики статического частотного уплотнения оказываются неудачными, можно легко продемонстрировать на примере простых вычислений теории массового обслуживания. Для начала сосчитаем среднее время задержки T для отправки кадра по каналу емкостью C бит/с. Предполагается, что кадры прибывают в случайном порядке со средней скоростью 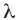 кадров в секунду. Длина кадров является случайной величиной, среднее значение которой равно
кадров в секунду. Длина кадров является случайной величиной, среднее значение которой равно 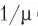 бита. При таких параметрах скорость обслуживания канала равна
бита. При таких параметрах скорость обслуживания канала равна 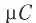 кадров в секунду. Теория массового обслуживания говорит о том, что
кадров в секунду. Теория массового обслуживания говорит о том, что
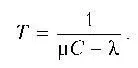
(Для любознательных: это результат для очереди M/M/1. Требуется, чтобы случайность длительности промежутков между кадрами и длины кадров соответствовали экспоненциальному распределению или, что эквивалентно, являлись результатом пуассоновского процесса.)
В нашем примере C равно 100 Мбит/с, средняя длина кадра 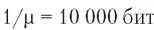 , ско
, ско
рость прибытия кадров X = 5000 кадров в секунду. Тогда T = 200 мкс. Обратите внимание: если бы мы не учли задержки при формировании очереди и просто посчитали, сколько времени нужно на передачу кадра длиной 10 000 бит по сети с пропускной способностью 100 Мбит/с, то получили бы неправильный ответ: 100 мкс. Это число приемлемо лишь при отсутствии борьбы за канал.
Теперь давайте разделим канал на N независимых подканалов, у каждого из которых будет пропускная способность C/N бит/с. Средняя входная скорость в каждом подканале теперь будет равна 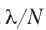 кадров в секунду. Сосчитав новое значение средней задержки T , получим:
кадров в секунду. Сосчитав новое значение средней задержки T , получим:
Читать дальше
Конец ознакомительного отрывка
Купить книгу

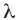 кадров в секунду. Длина кадров является случайной величиной, среднее значение которой равно
кадров в секунду. Длина кадров является случайной величиной, среднее значение которой равно 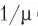 бита. При таких параметрах скорость обслуживания канала равна
бита. При таких параметрах скорость обслуживания канала равна 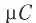 кадров в секунду. Теория массового обслуживания говорит о том, что
кадров в секунду. Теория массового обслуживания говорит о том, что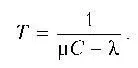
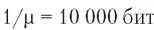 , ско
, ско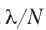 кадров в секунду. Сосчитав новое значение средней задержки T , получим:
кадров в секунду. Сосчитав новое значение средней задержки T , получим:







