Carroll Quigley - The Evolution of Civilizations

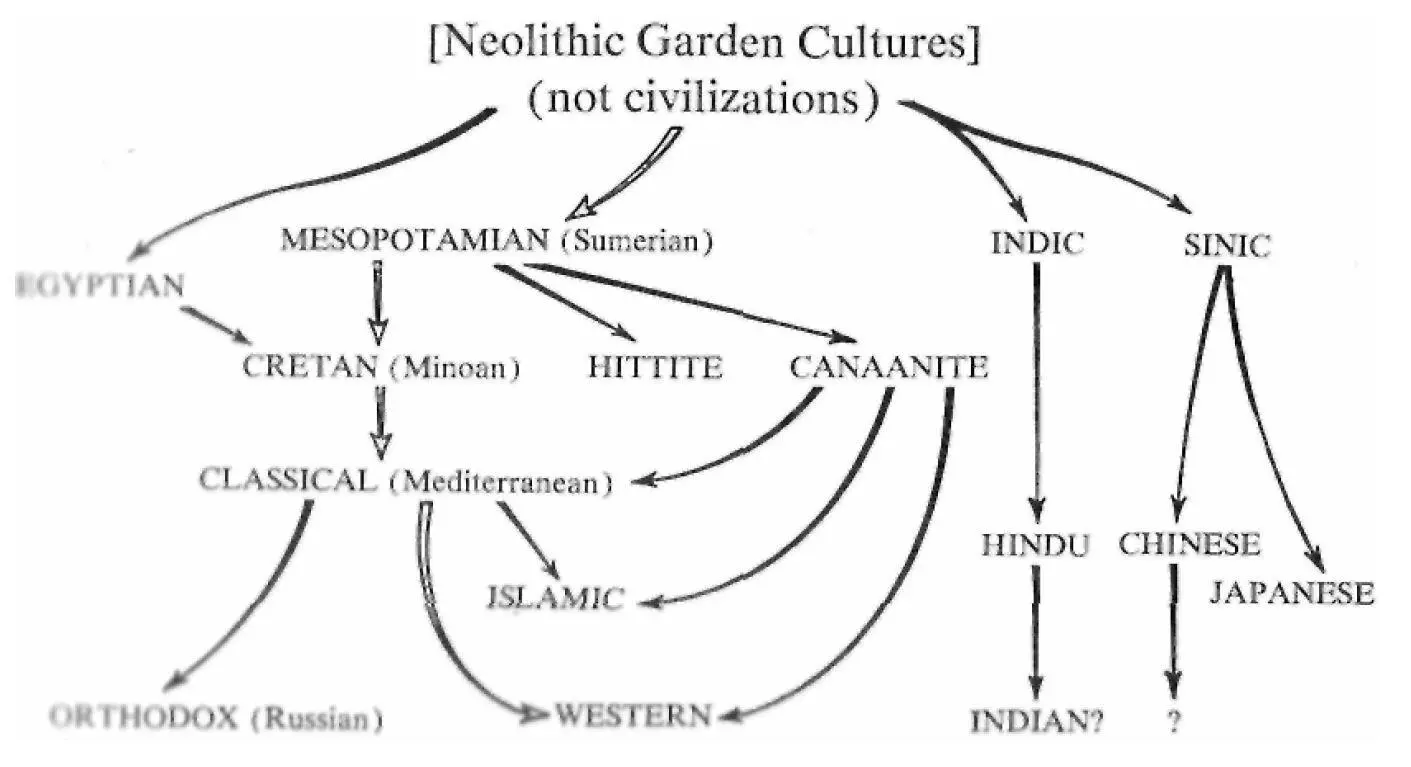
In this diagram the family tree of our own Western civilization (a lineage involving three generations between the Neolithic Garden cultures and ourselves) has been marked with a double line. The meaning behind these lines and the other cultural connections shown on the diagram will be indicated later.

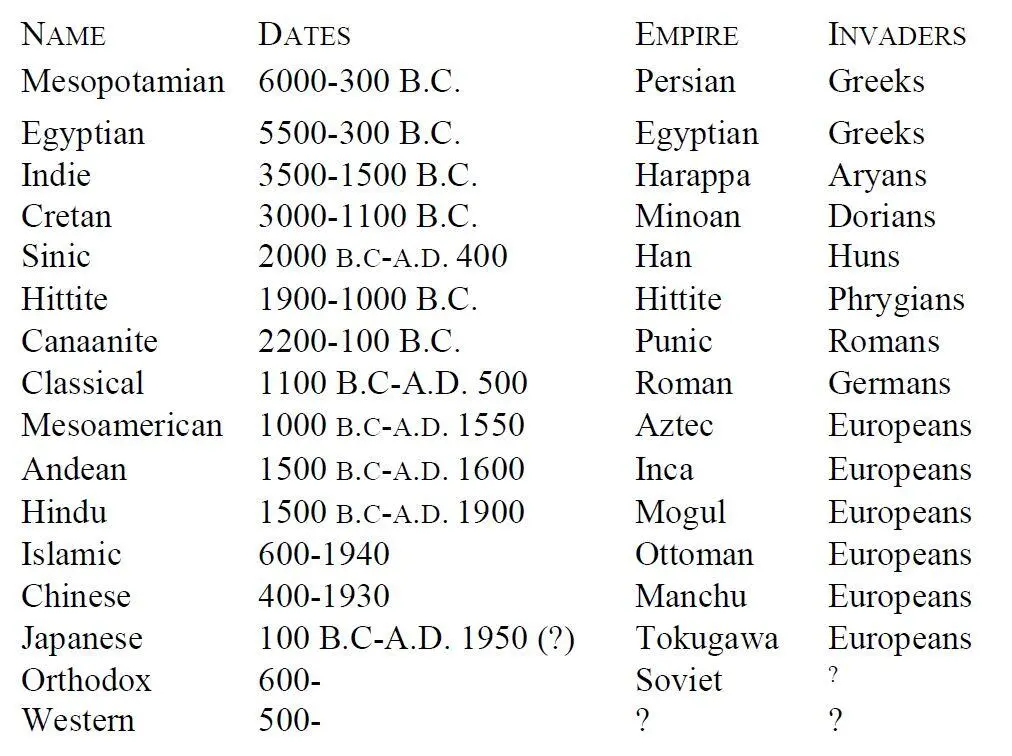
For later reference the following table gives the name, approximate dates, the name of the culminating empire, and the outside intruders who terminated its existence for the sixteen civilizations mentioned:

4. Historical Analysis

We have already mentioned our belief that civilization is an object that can be studied in a scientific way just as a quartz crystal can be studied. In such a study we must, like the student of crystals, examine in a comparative way a large number of examples—even, ideally, all the examples available. But it is obvious that a civilization is a much more complicated object than a crystal. Let us be explicit about that word "complicated." A civilization is complicated, in the first place, because it is dynamic; that is, it is constantly changing in the passage of time, until it has perished. Furthermore, a civilization is part of the social sciences; that is, it contains subjective elements, and these are usually the more important elements in the culture. Accordingly, in a civilization, unlike a crystal, what people think or feel can influence what exists, changing the object completely in the process. In the third place, many aspects of a civilization are continua, existing in such subtle gradations and in such varied degrees of abstractness that the divisions we make in it, in the course of our analysis, and the words we use as symbols to refer to our analytical divisions reflect only very roughly the situation that exists in the reality itself. All three of these difficulties are important, but the third, which is frequently ignored in discussions of these matters, requires a little further examination—for that reason, at least.

Much, if not all, of the physical world consists of continua. To say this is equivalent to saying that much of the physical world is irrational. It exists and it operates, but it does these things in ways that cannot be grasped by our conscious rational mental processes. This can be seen most easily if we consider first a few examples of continua in the physical world.

How many colors are there in a rainbow? Some answer three—red, yellow, blue. Others answer six—red, orange, yellow, green, blue, violet. When I was a child in school, for some unknown reason, we were told that there were seven colors, the teacher inserting "indigo" between blue and violet. The proper answer, of course, is that the number of colors in the rainbow is infinite. This in itself is something we cannot grasp in any rational way. But let us consider what it means.

In the first place it means that there is, in the rainbow, no real line of division between any two colors. If we wish to draw a line we may do so, but we must recognize that such a line is imaginary—it may exist in our minds, but it does not exist in the rainbow itself.

Moreover, any line that we draw is arbitrary, in the sense that it could have been drawn with just as much justification somewhere else, perhaps only a hairbreadth away. If we draw a line between red and orange and another between orange and yellow, we may call the gamut between those two lines orange, but, as a matter of fact, the color is quite different on either edge of that gamut. We may decide that orange is a narrower range than the gamut between our two lines and, accordingly, slice off the margins of the orange gamut, calling the severed margin on one side yellow-orange and the severed margin on the other side red-orange. But once again the color is not the same across any of these three ranges. In fact, it is impossible to cut off any gamut in a rainbow, no matter how narrow we make it, in which the color is the same across the width of the gamut. We can move no distance, however infinitesimally small it may be, across the rainbow without a change in color. This means that the number of colors in the rainbow is infinite. But it also means that the number of colors in any portion of the rainbow is infinite. That is, there are as many shades of orange as there are colors in the whole rainbow, since both are infinite. Now, this is a truth that we cannot understand rationally. It seems contrary to logic and reason that we could add all the existing shades of red and yellow to all the existing varieties of orange without increasing the number of color varieties we have. The reason is not so much that infinity added to infinity gives infinity as that there are no different varieties of colors at all, because there are, in fact, no dividing lines in the rainbow itself. When we use the plural terms "colors" and "shades" in reference to a rainbow, we are implying that there are different colors and accordingly that there are divisions in the rainbow somehow separating one shade from another and thus entitling us to speak of these in the plural. Since there are no such lines of separation, we would be more accurate if we spoke of the rainbow in the singular as "a continuum of color." But, of course, we could not do this consistently because it would make it impossible to think about or to talk about the colors of any objects. Since the continuum changes across its range, it is distinctly different in color from one portion to another, just as dresses, flowers, or neckties are different in color from one another. If we are going to talk about these very real differences, we must have different words for the different colors involved. Thus we must give different color terms to different portions of the rainbow's gamut. The important truth to remember is that, while the differences between colors are real enough, there are no real divisions between colors: these are arbitrary and imaginary.

As is well known, the gamut of radiations of visible light that we call the rainbow is not an entity in itself but is an arbitrary and imaginary portion cut out of a much wider gamut of electromagnetic radiations. The variety of colors in the rainbow arises from the fact that the radiations of visible light come at us in wave lengths of different frequency. As the wave lengths of these radiant forms of energy get smaller (and thus their frequency gets larger), we observe this difference as a shift in color toward the blue end of the visible spectrum; as the wave lengths get longer (and the frequency less), we observe a color shift toward the red end of the spectrum. If this shift of wave length continues, the radiation may pass beyond the range to which our eyes are sensitive. Beyond the red we can notice these radiations as heat (infrared); beyond the violet we might have difficulty noticing the radiations directly, but their consequence would soon appear as a kind of sunburn on our skin. Once again there is no dividing line between the visible gamut of radiations and the ultraviolet on one side and the infrared on the other side. Some persons can "see" further into these than others can, and other forms of living creatures can "see" further into one or the other range than any human could. Bees, for example, are fully sensitive to ultraviolet radiations, while humans are generally so insensitive to these that they consider glass windows, which cut off most ultraviolet, as being fully transparent.

The gamut of radiant energy is much wider than the three subgamuts we have mentioned. Beyond the invisible ultraviolet are other radiations of even shorter wave length, including soft X rays, hard X rays, and finally the very high-frequency gamma waves released by nuclear explosions. Going the other way in the radiation range, we find that there are radiations of increasing wave length beyond the infrared which we call heat. These radiations of lower frequency and longer wave length include those used to carry our radio and television broadcasts. While we sit here reading, quite unaware of their passage, these radiations are going through our bodies. They are different from the visible light that allows us to see to read only in the wave lengths and energy content of the radiations.