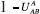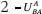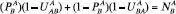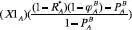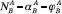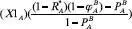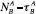Meanwhile, using data put together by my students, the game’s forecast was for failure at Copenhagen and that, sadly, is just what we got.
The predictions thus far have been pretty well borne out by subsequent events, so there is not much to be embarrassed about. Rather, the match between predictions and outcomes over the past year may be seen as encouraging to those who believe that through the transparent application of logic and evidence we can anticipate and perhaps influence the course of events for the better.
The model’s success continues to garner the attention of people making high-stakes decisions and is stimulating others to teach game-theory-based political forecasting. The model’s performance and online availability is even helping to bring this particular rational-actor approach into the classroom in new arenas, including graduate programs in social work, psychiatry, and business and in military training. That is most gratifying. With a bit of luck, we may see further integration of a more rational approach to how we understand the decisions and actions of others. Then we may be better able to use that understanding to inform our own decisions, corporate decisions, and decisions in the arena of national security, helping to make the world a more peaceful, more just, and happier place for all of us.
Bruce Bueno de Mesquita,
February 2010
Appendix

Because some of you asked for it:
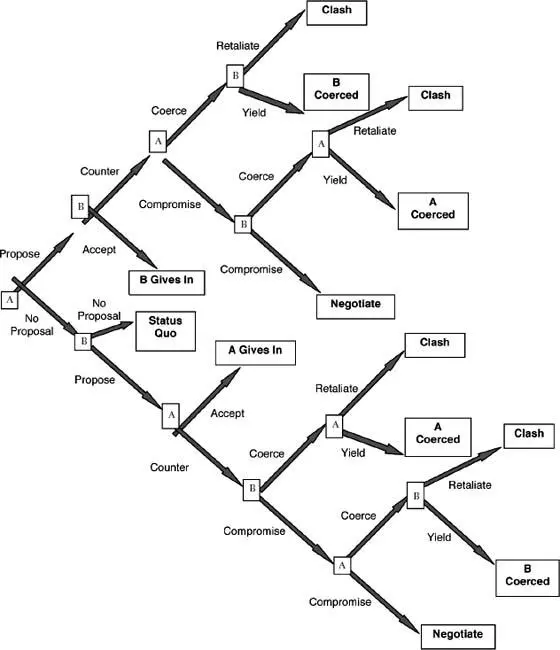
The figure below illustrates a single stage game for a single pair of players (call them A and B) while not displaying the sources of uncertainty in the model. Nature assigns initial probabilities of 0.5 to player types, and the model then applies Bayes’ Rule so that the players can update their beliefs. There are 16 possible combinations of beliefs about the mix of player types. Each player is uncertain whether the other player is a hawk or a dove or whether the other player is pacific or retaliatory. By hawk I mean someone who prefers to compel a rival to give in to the hawk’s demands even if this necessitates both imposing and enduring costs rather than compromising on the policy outcome. A dove prefers to compromise rather than engage in costly coercion to get the rival to give in. A retaliatory player prefers to defend itself – at potentially high costs – rather than be bullied into giving in while a pacific player prefers to give in to avoid further costs.
The game is iterated so that payoffs can change from round to round with a round defined as a sequence of moves through the stage game in the figure. Because the game is solved for all directional pairs it assumes that players do not know whether they will be moving first, second, or simultaneously with each other player. The game ends, by assumption, when the sum of player payoffs in an iteration is greater than the projected sum of those payoffs in the next iteration.
Structure of the Game: Sketch of One of N 2− N Stage Games Played Simultaneously
A and B uncertain whether other will retaliate if coerced
A and B uncertain whether other will coerce if given the chance In playing the game, each player’s initial move is to choose whether to make proposals. A proposal is expressed as a demand that another player accept some specific change in his position that is favorable to the demander. Players choose proposals designed to maximize their welfare at the end of the stage game. In practice, this means choosing proposals that make the other players indifferent between imposing costs on the demander and preferring a negotiated compromise instead. Of course, the endogenous selection of proposal values must take into account player beliefs about their rival’s type.
Payoffs are calculated as follows:
Let the probability that A prevails in an iteration of the game vs. B =
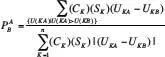
where K are all of the stakeholders, C is the potential clout or influence of each stakeholder, S is the salience each stakeholder attaches to the issue, and U denotes utility with the first subscript indicating whose utility is being evaluated and the second vis-à-vis which other player’s approach to the issue.
Let X1k = player K’s policy preference on the issue; Let X2k = player K’s preference over reaching agreement or being resolute on the issue. Let A’s utility for the status quo = 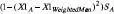
Let A’s utility for B’s approach to the issue =
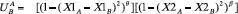 with
with 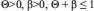 ; that is, the model assumes that players prefer a mix of gains based on sharing resolve or flexibility to settle and based on the issue outcome sought over fully satisfying themselves on one dimension while getting nothing on the other. The structure of the utility of proposals is comparably computed but with positions chosen endogenously rather than necessarily being either player’s policy position.
; that is, the model assumes that players prefer a mix of gains based on sharing resolve or flexibility to settle and based on the issue outcome sought over fully satisfying themselves on one dimension while getting nothing on the other. The structure of the utility of proposals is comparably computed but with positions chosen endogenously rather than necessarily being either player’s policy position.
The model assumes 4 sources of costs:
(1)α, the cost of trying to coerce and meeting resistance; (2)ι, the cost of being coerced and resisting; (3)γ, the cost of being coerced and not resisting; and (4)φ, the cost of coercing; that is, the cost of failing to make a credible threat that leads the foe to acquiesce. It also allows all of the input variables to change (doing so in accordance with heuristic rules I impose on the game). That is, the model is designed so that player clout, salience, resolve and position shift from iteration to iteration in response to the equilibrium conditions of the prior round of play. Because alternative heuristic rules chosen by others are likely to be as sensible and reliable as mine either for evaluating costs or for assessing how variable values change across periods of play, I do not dwell here on those aspects of the model.
With these values in hand, here are the expected payoffs at terminal nodes in the first iteration:
Let A’s utility for its initial demand/proposal to B= 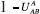
Let A’s utility for B’s initial demand/proposal to A = 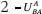
Let 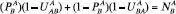
Outcome = B Gives In: A’s proposal = 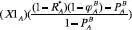
Outcome = A Coerces, B Resists: A’s expected payoff if A tries to coerce and B resists: 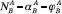
Outcome = A Coerces, B Yields: A’s proposal = 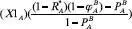
Outcome = B Coerces, A Resists: A’s expected payoff if B tries to coerce A and B resists 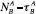
Читать дальше



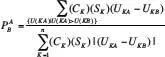
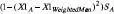
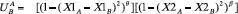 with
with 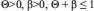 ; that is, the model assumes that players prefer a mix of gains based on sharing resolve or flexibility to settle and based on the issue outcome sought over fully satisfying themselves on one dimension while getting nothing on the other. The structure of the utility of proposals is comparably computed but with positions chosen endogenously rather than necessarily being either player’s policy position.
; that is, the model assumes that players prefer a mix of gains based on sharing resolve or flexibility to settle and based on the issue outcome sought over fully satisfying themselves on one dimension while getting nothing on the other. The structure of the utility of proposals is comparably computed but with positions chosen endogenously rather than necessarily being either player’s policy position.