Неизвестно - Prolog

Давайте проиллюстрируем этот принцип на примере. Предположим, что мы хотим доказать, что теоремой является следующая пропозициональная формула:

( а => b ) & ( b => с ) => ( а => с )

Смысл этой формулы таков: если из а следует b и из b следует с , то из а следует с .

Прежде чем начать применять процесс резолюции ("резолюционный процесс"), необходимо представить

отрицание нашей формулы в наиболее приспособленной для этого форме. Такой формой является

конъюнктивная нормальная форма

, имеющая вид

( р 1 v p 2 v ...) & ( q 1 v q 2 v ...)

& ( r 1 v r 2 v ...) & ...

Здесь р i , q i , r i - элементарные утверждения

или их отрицания. Конъюнктивная нормальная форма есть конъюнкция членов, называемых

дизъюнктами

, например (

p 1

v

p 2

v ...) - это дизъюнкт.

Любую пропозициональную формулу нетрудно преобразовать в такую форму. В нашем случае это делается следующим образом. У нас есть исходная формула

( а => b ) & ( b => с ) => ( а => с )

Ее отрицание имеет вид

~ ( ( а => b ) & ( b => с ) => ( а => с ) )

Для преобразования этой формулы в конъюнктивную нормальную форму можно использовать следующие известные правила:

(1) х => у эквивалентно ~х v у

(2) ~ ( x v y ) эквивалентно ~х & ~у

(3) ~ ( х & у ) эквивалентно ~х v ~у

(4) ~ ( ~х ) эквивалентно х

Применяя правило 1, получаем

~ ( ~ ( ( a => b ) & ( b => с )) v ( а => с ) )

Далее, правила 2 и 4 дают

( а => b ) & ( b => с ) & ~( а => с )

Трижды применив правило 1, получаем

( ~ а v b ) & ( ~b v с ) & ~ ( ~а v с )

И наконец, после применения правила 2 получаем искомую конъюнктивную нормальную форму

( ~а v b ) & ( ~b v с ) & а & ~с

состоящую из четырех дизъюнктов. Теперь можно приступить к резолюционному процессу

.

Элементарный шаг резолюции выполняется всегда, когда имеется два дизъюнкта, в одном из которых встретилось элементарное утверждение р , а в другом - ~р . Пусть этими двумя дизъюнктами будут

р v Y и ~р v

Z

Шаг резолюции порождает третий дизъюнкт:

Y v Z

Нетрудно показать, что этот дизъюнкт логически следует из тех двух дизъюнктов, из которых он получен. Таким образом, добавив выражение ( Y v Z ) к нашей исходной формуле, мы не изменим ее истинности. Резолюционный процесс порождает новые дизъюнкты. Появление "пустого дизъюнкта" (обычно записываемого как "nil") сигнализирует о противоречии. Действительно, пустой дизъюнкт nil порождается двумя дизъюнктами вида

x и ~x

которые явно противоречат друг другу.

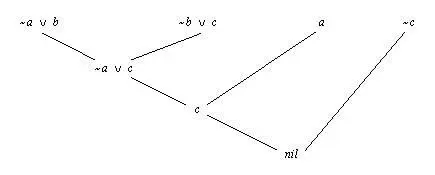
Рис. 16. 6. Доказательство теоремы ( а=>b )&( b=>с )=>( a=>с ) методом

резолюции. Верхняя строка - отрицание теоремы в конъюнктивной

нормальной форме. Пустой дизъюнкт внизу сигнализирует, что

отрицание теоремы противоречиво.

На рис. 16.6 показан процесс применения резолюций, начинающийся с отрицания нашей предполагаемой теоремы и заканчивающийся пустым дизъюнктом.

На рис. 16.7 мы видим, как резолюционный процесс можно сформулировать в форме программы, управляемой образцами. Программа работает с дизъюнктами, записанными в базе данных. В терминах образцов принцип резолюции формулируется следующим образом:

если

существуют два таких дизъюнкта С1 и С2 , что

P является (дизъюнктивным) подвыражением С1 ,

а ~Р - подвыражением С2

то

удалить Р из С1 (результат - СА ), удалить ~Р

из С2 (результат - СВ ) и добавить в базу

данных новый дизъюнкт СА v СВ .

На нашем формальном языке это можно записать так:

[ дизъюнкт( С1), удалить( Р, Cl, CA),

дизъюнкт( С2), удалить( ~Р, С2, СВ) ] --->

[ assert( дизъюнкт( СА v СВ) ) ].

Это правило нуждается в небольшой доработке. Дело в том, что мы не должны допускать повторных взаимодействий между дизъюнктами, так как они порождают новые копии уже существующих формул. Для этого в программе рис. 16.7 предусматривается запись в базу данных информации об уже произведенных взаимодействиях в форме утверждений вида

сделано( Cl, C2, Р)

В условных частях правил производится распознавание подобных утверждений и обход соответствующих повторных действий.