Неизвестно - Prolog

Проиллюстрируем этот подход на классическом примере. Пусть имеются следующие аксиомы:

Все люди смертны.

Сократ - человек.

Теорема, логически вытекающая из этих двух аксиом:

Сократ смертен.

Первую из вышеуказанных аксиом можно переписать так:

Для всех X, если X - человек, то X смертен.

Соответственно наш пример можно перевести на Пролог следующим образом:

смертен( X) :- человек( X). % Все люди смертны

человек( сократ). % Сократ - человек

?- смертен( сократ). % Сократ смертен?

yes (да)

Более сложный пример из программы о родственных отношениях, приведенной на рис. 1.8:

?- предок( том, пат)

Мы знаем, что родитель( боб, пат)- это факт. Используя этот факт и правило пр1 , мы можем сделать вывод, что утверждение предок( боб, пат)истинно. Этот факт получен в результате вывода - его нельзя найти непосредственно в программе, но можно вывести, пользуясь содержащимися в ней фактами и правилами. Подобный шаг вывода можно коротко записать

родитель( боб, пат) ==> предок( боб, пат)

Эту запись можно прочитать так: из родитель( боб, пат)следует предок( боб, пат)на основании правила пр1 . Далее, нам известен факт родитель( том, боб). На основании этого факта и выведенного факта предок( боб, пат)можно заключить, что, в силу правила пр2 , наше целевое утверждение предок( том, пат)истинно. Весь процесс вывода, состоящий из двух шагов, можно записать так:

родитель(боб, пат) ==> предок( боб, пат)

родитель(том, боб) и предок( боб, пат) ==>

предок( том, пат)

Таким образом, мы показали, какой может быть последовательность шагов для достижения цели, т.е. для демонстрации истинности целевого утверждения. Назовем такую последовательность цепочкой доказательства. Однако мы еще не показали как пролог-система в действительности строит такую цепочку.

Пролог-система строит цепочку доказательства в порядке, обратном по отношению к тому, которым мы только что воспользовались. Вместо того, чтобы начинать с простых фактов, приведенных в программе, система начинает с целей и, применяя правила, подменяет текущие цели новыми, до тех пор, пока эти новые цели не окажутся простыми фактами. Если задан вопрос

?- предок( том, пат).

система попытается достичь этой цели. Для того, чтобы это сделать, она пробует найти такое предложение в программе, из которого немедленно следует упомянутая цель. Очевидно, единственными подходящими для этого предложениями являются пр1 и пр2 .

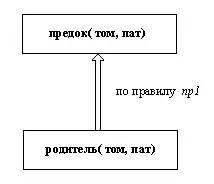
Рис. 1. 9. Первый шаг вычислений. Верхняя цель истинна, если истинна нижняя.

Это правила, входящие в отношение предок. Будем говорить, что головы этих правил сопоставимы с целью.

Два предложения пр1 и пр2 описывают два варианта продолжения рассуждений для пролог-системы. Вначале система пробует предложение, стоящее в программе первым:

предок( X, Z) :- родитель( X, Z).

Поскольку цель - предок( том, пат), значения переменным должны быть приписаны следующим образом:

X = том, Z = пат

Тогда исходная цель предок( том, пат)заменяется новой целью:

родитель( том, пат)

Такое действие по замене одной цели на другую на основании некоторого правила показано на рис. 1.9. В программе нет правила, голова которого была бы сопоставима с целью родитель(том, пат), поэтому такая цель оказывается неуспешной. Теперь система делает возврат к исходной цели, чтобы попробовать второй вариант вывода цели верхнего уровня предок( том, пат). То есть, пробуется правило пр2 :

предок( X, Z) :-

родитель( X, Y),

предок( Y, Z).

Как и раньше, переменным X и Z приписываются значения:

X = том, Z = пат

В этот момент переменной Y еще не приписано никакого значения. Верхняя цель предок( том, пат)заменяется двумя целями:

родитель( том, Y),

предок( Y, пат)

Этот шаг вычислений показан на рис. 1.10, который представляет развитие ситуации, изображенной на рис. 1.9.

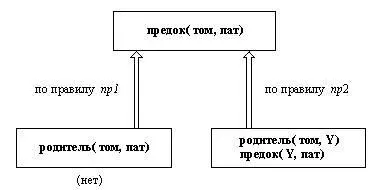
Рис. 1. 10. Продолжение процесса вычислений, показанного на рис. 1.9.