Feynmann - Feynmann 7

Если третий слой имеет атом в точке В, кристаллическая решетка будет гранецентрированной кубической, но видно это под некоторым углом. Забавно, что, начав с шестиугольни­ков, можно прийти к кубической структуре. Но обратите вни­мание, что куб, рассматриваемый под определенным углом, имеет очертания шестиугольника. Например, фиг. 30.6 может изображать либо плоский шестиугольник, либо и куб в пер­спективе!

Если к фиг. 30.5, б добавляется третий слой, начиная с ато­ма в точке А, то кубической структуры не возникает и у ре­шетки будет только гексагональная симметрия. Ясно, что обе опи­санные нами возможности дают одинаковую плотную упаковку.

Некоторые металлы (например, серебро и медь) выбирают первую альтернативу — решетка у них гранецентрированная кубическая. Другие же (например, бериллий и магний) пред­почитают вторую возможность и образуют гексагональные кристаллы. Очевидно, появление той или иной решетки не может зависеть только от способа упаков­ки маленьких шариков, но должно еще определяться и другими факторами. В частности, оказывается существенной небольшая угловая зависимость межатомных сил (или в случае металлов от энергии электронного океана).

Фиг. 30.6. Что это — шестиугольник или куб?

Все эти вещи вы несомненно узнаете из курса химии.

§ 5. Симметрии в двух измерениях

Теперь мне хотелось бы обсудить некоторые свойства кри­сталлов с точки зрения их внутренних симметрии. Основное свойство кристалла состоит в том, что если вы сдвинетесь от одного атома на один период решетки к соответствующему ато­му, то попадете в точно такое же окружение. Это фундамен­тальное утверждение. Но если бы вы сами были атомом, то могли бы заметить другое передвижение, которое привело бы вас в точно такое же окружение, т. е. в другую возможную «симмет­рию». На фиг. 30.7, а показан еще один возможный узор обоев (хотя вы, наверно, такого никогда не видали).

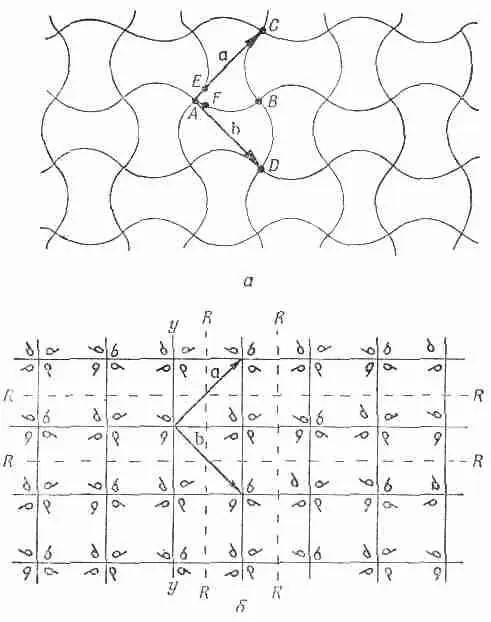
Фиг. 30.7. Узор обоев с высокой симметрией.

Предположим, что мы сравниваем окру­жения в точках А и В. Вы могли бы сперва подумать, что они одинаковы. Не совсем. Точки С и D экви­валентны А, но окружение В подобно А, только если все рядом обращать как будто в зеркале.

В этом узоре имеются еще и другие виды «эквивалентных» точек. Так, точки Е и F обладают «одинаковыми» окружениями, за тем исключением, что одно повернуто на 90° по отношению к другому. Узор особенный. Вращение на 90°, проделанное сколько угодно раз вокруг такой вершины, как A, снова дает тот же узор. Кристалл с такой структурой имел бы на поверхнос­ти прямые углы, но внутри он устроен сложнее, чем простой куб.

Теперь, когда мы описали ряд частных случаев, попытаемся вывести все возможные типы симметрии, какие может иметь кристалл. Прежде всего посмотрим, что получается в плоскости. Плоская решетка может быть определена с помощью двух так называемых основных векторов, которые идут от одной точки решетки к двум ближайшим эквивалентным точкам. Два вектора 1 и 2 суть основные векторы решетки на фиг. 30.1. Два век­тора а и b на фиг. 30.7, а — основные векторы для изображен­ного там узора. Мы могли бы, конечно, с тем же успехом заме­нить а на -а или bна - b. Раз аи bодинаковы по величине и перпендикулярны друг другу, то вращение на 90° переводит а в b и b в а и снова дает ту же решетку.

Итак, мы видим, что существуют решетки, обладающие «четырехсторонней» симметрией. А раньше мы описали плотную упаковку, основанную на шестиугольнике и обладающую шестисторонней симметрией. Вращение набора кружков на фиг. 30.5, а на угол 60° вокруг центра любого шарика пере­водит рисунок сам в себя.

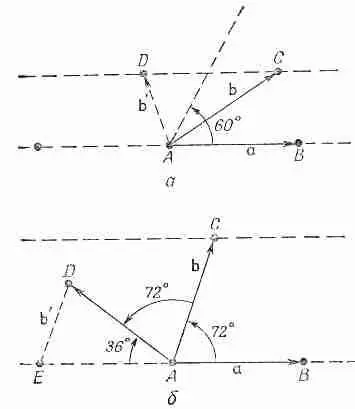
Какие виды вращательной симметрии существуют еще? Может ли быть, например, вращательная симметрия пятого или восьмого порядка? Легко понять, что они невозможны. Единственная симметрия, связанная с фигурой, имеющей более четырех сторон, есть симметрия шестого порядка. Прежде всего покажем, что симметрия более чем шестого порядка невозмож­на. Попытаемся вообразить решетку с двумя равными основ­ными векторами, образующими угол менее 60° (фиг. 30.8, а).