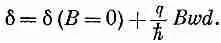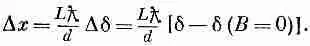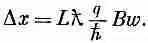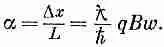Feynmann - Feynmann 6

А тогда поле А в нашем смысле уже «реально». Вы можете возразить: «Но ведь там есть магнитное поле». Да, есть, но вспомните нашу исходную идею — «реально» только такое поле, которое, чтобы определить собой движение частицы, должно быть задано в том месте, где она находится. Поле В в нити действует на расстоянии. Если мы не хотим, чтобы его влияние выглядело как действие на расстоянии, мы должны пользо­ваться векторным потенциалом.

Эта проблема имеет интересную историю. Теория, которую мы изложили, была известна с самого возникновения квантовой механики, с 1926 г. Сам факт, что векторный потенциал появ­ляется в волновом уравнении квантовой механики (так назы­ваемом уравнении Шредингера), был очевиден с того момента, как оно было написано. В том, что он не может быть заменен магнитным полем, убеждались все, кто пытался это проделать; друг за другом все убеждались, что простого пути для этого не существует. Это ясно и из нашего примера, когда электрон движется по области, где нет никакого поля, и тем не менее подвергается воздействию. Но, поскольку в классической механике А, по-видимому, не имело непосредственного, важного значения и, далее, из-за того, что его можно было менять добав­лением градиента, люди еще и еще раз повторяли, что вектор­ный потенциал не обладает прямым физическим смыслом, что даже в квантовой механике «правами» обладают только элект­рические и магнитные поля. Когда оглядываешься назад, ка­жется странным, что никто не подумал обсудить этот опыт вплоть до 1956 г., когда Бом и Аронов впервые предложили его и сделали весь вопрос кристально ясным. Все это ведь всегда подразумевалось, но никто не обращал на это внимания. И мно­гие были просто потрясены, когда всплыл этот вопрос. Вот по этой-то причине кое-кто и счел нужным поставить опыт и убе­диться, что все это действительно так, хотя квантовая меха­ника, в которую все мы верим вот уже сколько лет, давала вполне недвусмысленный ответ. Занятно, что подобные вещи могут тридцать лет быть на виду у всех, но из-за определенных предрассудков относительно того, что существенно, а что нет, могут всеми игнорироваться.

Сейчас мы хотим немного продолжить наш анализ. Мы продемонстрируем связь между квантовомеханической и класси­ческой формулами, чтобы показать, почему оказывается, что при макроскопическом взгляде на вещи все выглядит так, как будто частицы управляются силой, равной произведению qv на ротор А. Чтобы получить классическую механику из кванто­вой, нам нужно рассмотреть случаи, когда все длины волн малы по сравнению с расстояниями, на которых заметно ме­няются внешние условия (например, поля). Мы не будем гнаться за общностью доказательства, а только покажем все на очень простом примере. Обратимся снова к тому же опыту со щелями. Но теперь вместо того, чтобы втискивать все маг­нитное поле в узкий промежуток между щелями, представим себе такое магнитное поле, которое раскинулось позади щелей широкой полосой (фиг. 15.8). Возьмем идеализированный слу­чай, когда в узкой полосе шириной w , много меньшей L, маг­нитное поле однородно. (Это легко устроить, надо только по­дальше отнести поглотитель.) Чтобы подсчитать сдвиг по фазе, мы должны взять два интеграла от А вдоль двух траекторий (1) и (2).

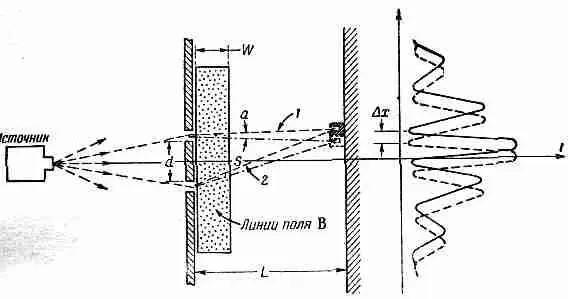
Фиг. 15.8. Сдвиг интерференционной картины из-за наличия полоски магнитного поля.

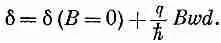
Как мы видели, они различаются просто на поток В между этими путями. В нашем приближении поток равен B w d . Раз­ность фаз для двух путей поэтому равна

(15.37)

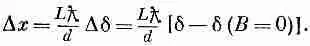
Мы замечаем, что в принятом приближении сдвиг фаз не зави­сит от угла. Так что опять-таки эффект сводится к сдвигу всей картины вверх на величину D х. Из формулы (15.28)

Подставляя d-d (В = 0) из (15.37), получаем

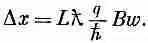
(15.38)

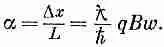
Такой сдвиг равноценен тому, что все траектории отклоняются на небольшой угол а (см. фиг. 15.8), равный

(15.39)