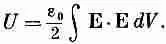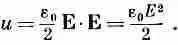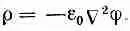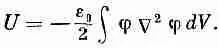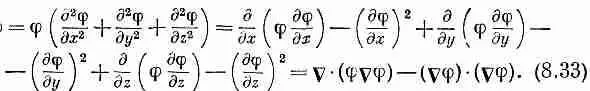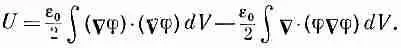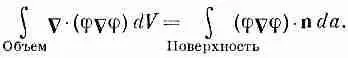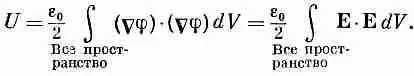Feynmann - Feynmann 5a

Имеется и физический резон в требовании, чтобы мы были в состоянии указать, где именно заключена энергия. По теории тяготения всякая масса есть источник гравитационного притя­жения. А по закону Е=тс 2 мы также знаем, что масса и энергия вполне равноценны друг другу. Стало быть, всякая энергия яв­ляется источником силы тяготения. И если б мы не могли узнать, где находится энергия, мы бы не могли знать, где расположена масса. Мы не могли бы сказать, где размещаются источники поля тяготения. И теория тяготения стала бы неполной.

Конечно, если мы ограничимся электростатикой, то способа узнать, где сосредоточена энергия, у нас нет. Но полная система максвелловских уравнений электродинамики снабдит нас не­сравненно более полной информацией (хотя и тогда, строго говоря, ответ до конца определенным не станет). Подробнее мы этот вопрос рассмотрим позже. А сейчас приведем лишь результат, касающийся частного случая электростатики

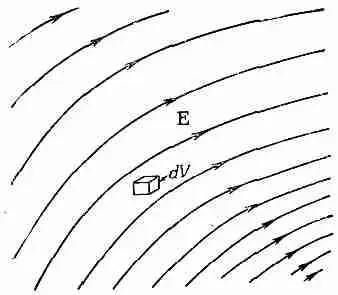
Фиг. 8.8. Каждый элемент объема dV = dxdydz в электриче­ском поле содержит в себе энер­гию (e 0/2) E 2 dV .

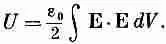
Энергия заключена в том пространстве, где имеется электрическое поле. Это, ви­димо, вполне разумно, потому что известно, что, ускоряясь, заряды излучают электрические поля. И когда свет или радио­волны распространяются от точки к точке, они переносят с со­бой свою энергию. Но в этих волнах нет зарядов. Так что энер­гию хотелось бы размещать там, где есть электромагнитное поле, а не там, где есть заряды, создающие это поле. Таким об­разом, мы описываем энергию не на языке зарядов, а на языке создаваемых ими полей. Действительно, мы можем показать, что уравнение (8.28) численно совпадает с

(8.30)

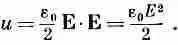
Эту формулу можно толковать, говоря, что в том месте простран­ства, где присутствует электрическое поле, сосредоточена и энергия; плотность ее (количество энергии в единице объема) равна

(8.31)

Эта идея иллюстрируется фиг. 8.8.

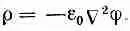
Чтобы показать, что уравнение (8.30) согласуется с нашими законами электростатики, начнем с того, что введем в уравне­ние (8.28) соотношение между r и j, полученное в гл. 6:

Получим

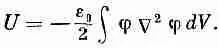
(8.32)

Расписав покомпонентно подынтегральное выражение, мы

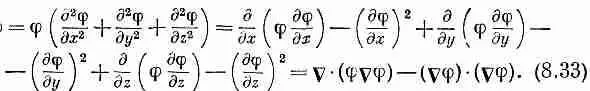
увидим, что

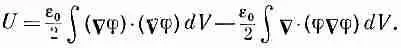
А наш интеграл энергий тогда равен

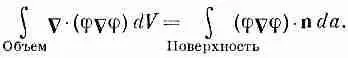
С помощью теоремы Гаусса второй интеграл можно превратить в интеграл по поверхности:

(8.34)

Этот интеграл мы подсчитаем для того случая, когда поверх­ность простирается до бесконечности (так что интеграл по объе­му обращается в интеграл по всему пространству), а все заряды расположены на конечном расстоянии друг от друга. Проще всего это сделать, взяв поверхность сферы огромного радиуса с центром в начале координат. Мы знаем, что вдали от всех заря­дов j изменяется как 1/R, a Сj как 1/ R 2 . (И даже быстрее, если суммарный заряд нуль.) Площадь же поверхности большой сферы растет только как R 2, так что интеграл по поверхности убывает по мере возрастания радиуса сферы как

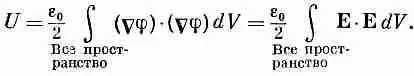
(1/R)(1/R 2)/R 2= (1/ R ). Итак, если наше интегрирование захватит собой все пространство (R® Ґ), то поверхностный интеграл обратится в нуль, и мы обнаружим

(8.35)

Мы видим, что существует возможность представить энергию произвольного распределения зарядов в виде интеграла от плотности энергии, сосредоточенной в поле.

§ 6. Энергия точечного заряда

Новое соотношение (8.35) говорит нам, что даже у отдель­ного точечного заряда q имеется какая-то электростатическая энергия. Поле в этом случае дается выражением