Feynmann - Feynmann 5

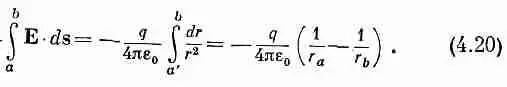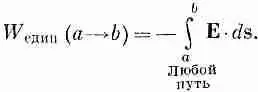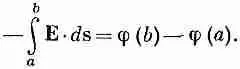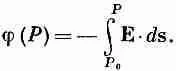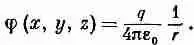
Посмотрим сначала, что происходит в поле, созданном еди­ничным зарядом q . Пусть точка а удалена от q на расстояние r 1, а точка b — на расстоя­ние r 2.

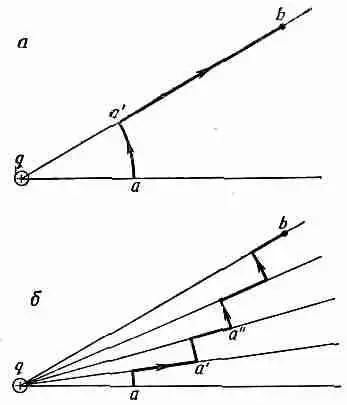
Фиг. 4.3. При переносе проб­ного заряда от а к b по любому пути тратится одна и та же работа.

Перенесем теперь другой заряд, называемый «пробным» и равный еди­нице, от а до b . Изберем сперва самый легкий для расчета путь. Перенесем наш пробный заряд снача­ла по дуге круга, а после no радиусу (фиг. 4.3, а).

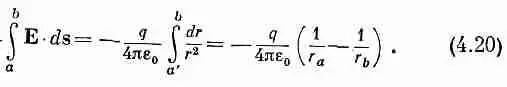
Рассчитать работу переноса по такому пути - детская забава (а иначе бы мы его и не выбрали). Во-первых, на участке aa ' работа не производится. Поле по закону Кулона радиально, т. е. направлено поперек направления движения. Во-вторых, на участке a ' b поле меняется как 1/r 2и направлено по движению. Так что работа переноса пробного заряда от а к b равна

Выберем теперь другой легкий путь, скажем тот, который изображен на фиг. 4.3, б. Он идет попеременно то по дуге ок­ружности, то по радиусу. Каждый раз, когда путь пролегает по дуге, никакой работы не затрачивается. Каждый раз, когда путь идет по радиусу, интегрируется 1/r 2. По первому радиаль­ному участку интеграл берется от r a до r a ’., по следующему — от r а . до r а "и т. д. Сумма всех таких интегралов как раз равна одному интегралу, но в пределах от r а до r b . В общем получится тот же ответ, что и в первом испробованном нами пути. Ясно, что и для любого пути, составленного из произвольного числа участков такого вида, получится тот же результат.

Ну а как насчет плавных траекторий? Получим ли мы тот же ответ? Этот вопрос мы обсудили в вып. 1, гл. 13. Пользуясь теми же доводами, что и тогда, мы можем заключить, что работа переноса единичного заряда от а до b от пути не зависит:

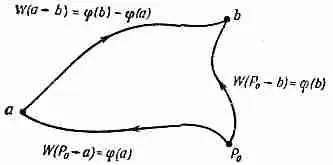
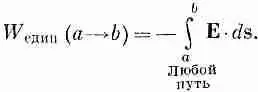
Фиг. 4.4. Работа, затрачен­ная на движение вдоль любого пути от а до b , равна минус работе от некоторой точки Р 0 до а плюс работа от Р 0 до b .

А раз выполняемая работа зависит только от концов пути, то она может быть представлена в виде разности двух чисел. В этом можно убедиться следующим образом. Выберем отправ­ную точку Р 0 и договоримся оценивать наш интеграл, пользуясь только теми траекториями, которые проходят через точку Р 0 . Обозначим работу, выполненную при движении против поля от Р 0 до точки а, через j(а), а работу на участке от Р 0 до точки b — через j(b) (фиг. 4.4). Работа перехода от а к Р 0 (по дороге к b ) равна j (a) с минусом, так что

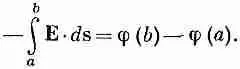
(4.21)

Так как повсюду будет встречаться только разность значе­ний функции j в двух точках, то положение точки Р 0 в сущности безразлично. Однако как только отправная точка выбрана, число j тем самым определяется в любой точке пространства; значит, j является скалярным полем, функцией от х, у, z . Эту скалярную функцию мы называем электростатическим потен­циалом в произвольной точке.

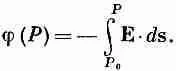
Электростатический потенциал

(4.22)

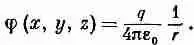
Часто очень удобно брать отправную точку на бесконеч­ности. Тогда потенциал jодиночного заряда в начале коорди­нат, взятый в произвольной точке (х, у, z), равен [см. уравнение (4.20)]

(4.23)

Электрическое поле нескольких зарядов можно записать в виде суммы электрических полей от первого заряда, от вто­рого, от третьего и т. д. Интегрируя сумму для того, чтобы определить потенциал, мы придем к сумме интегралов. Каждый из них — это потенциал соответствующего заряда. Значит, по­тенциал j множества зарядов есть сумма потенциалов каждого из зарядов по отдельности. Таким образом, и для потенциалов существует принцип наложения. Пользуясь такими же аргу­ментами, как и тогда, когда мы искали электрическое поле группы зарядов или распределения зарядов, мы можем полу­чить окончательные формулы для потенциала j в точке, обозна­ченной как (1):