Feynmann - Feynmann 4a

Представьте себе, что какой-то озорной чертик, решив под­шутить над физиками, пробрался во все лаборатории и всюду заменил слово «правое» на «левое». И в результате, где было написано правило правой руки, мы вынуждены были бы поль­зоваться правилом левой руки. Ну что ж, физики бы просто не заметили этого, ибо ни к какому изменению в физических за­конах это бы не привело, разумеется, если физические законы симметричны.

Покажем это на примере. Вы знаете, что существуют два сорта векторов. Имеются обыкновенные, «настоящие» векторы, подобные, например, отрезку расстояния Dr в пространстве. Пусть в нашей аппаратуре что-то находится «здесь», а нечто другое — «там», тогда те же самые «что-то» будут присутство­вать и в зеркально отраженной аппаратуре. Если мы в обоих случаях проведем векторы от «сюда» до «туда», то один вектор будет отражением другого (фиг. 52.2), причем направление стрелки вектора точно, как и все пространство, «выворачивает­ся наизнанку».

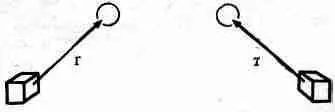
Фиг . 52.2. Отрезок в простран­стве и его зеркальное отраже­ние.

Такие векторы мы называем полярными.

Но второй сорт векторов, связанных с вращением, имеет совсем другую природу. Представьте себе нечто вращающееся в трехмерном пространстве (фиг. 52.3).

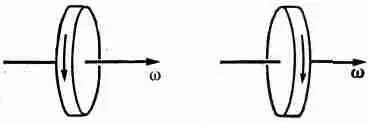
Фиг. 52.3. Вращающееся колесо и его зеркальное от­ражение.

Заметьте , что направление «вектора» угловой скорости т изменяется.

Если посмотреть на это в зеркало, то вращение будет происходить так, как показано на рисунке, т. е. как зеркальное изображение первоначального вращения. Условимся теперь представлять зеркальное враще­ние с помощью того же самого правила. В результате мы полу­чим «вектор», который в отличие от полярного вектора не изме­няется при отражении и оказывается перевернутым по отно­шению к полярному вектору и геометрии всего пространства. Такой вектор мы называем аксиальным.

Если физический закон симметрии относительно отражения правилен, то уравнения должны быть устроены так, чтобы при изменении знака каждого аксиального вектора и каждого век­торного произведения (что соответствует отражению) ничего не произошло. Например, когда мы пишем формулу для момента количества движения L= rX p, то здесь все в порядке, потому что при переходе в левую систему координат мы изменяем знак L, а знак ри rне изменяется. Кроме того, изменится и векторное произведение, поскольку мы должны правило правой руки за­менить правилом левой руки. Возьмем другой пример.

Известно, что сила, действующая на заряд в магнитном поле, равна F=q vX В, но если мы от правой системы перей­дем к левой, то, поскольку, как известно, Fи v— поляр­ные векторы, изменение знака из-за наличия векторного произведения должно компенсироваться изменением знака В, а это означает, что В должен быть аксиальным вектором. Дру­гими словами, при таком отражении Вдолжен переходить в — В. Таким образом, если мы изменяем левые координаты на правые, то одновременно нужно северный полюс магнита изменить на южный.

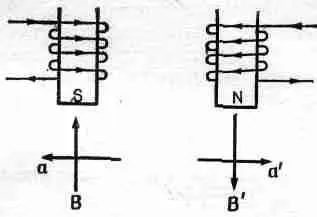
Давайте посмотрим на примере, как это все получается. Пусть у нас имеются два магнита, похожих на изображенные на фиг. 52.4.

Фиг. 52.4. Электромагнит и его зеркальное отражение.

Один из магнитов выглядит в точности так, как зеркальное отражение другого, т. е. витки его накручены в дру­гую сторону, и все, что происходит внутри катушки, должно быть в точности обращено в другую сторону; ток течет, как это показано на рисунке. Теперь из законов магнетизма (которые вы хотя еще и не знаете официально, но, по-видимому, помните из школьного курса) получается, что магнитное поле направлено так, как это показано на рисунке. Там, где у первого магнита южный полюс, у другого магнита будет северный, ибо у него ток течет в другую сторону, а магнитное поле перевернуто. Таким образом, выходит, что при переходе от правой системы к левой мы действительно должны заменить северный полюс на южный!

Но северный и южный полюсы — это просто договоренность, и замена их еще ничего не означает. Давайте посмотрим на само явление. Предположим, что электрон движется от нас через маг­нитное поле перпендикулярно к плоскости страницы. Тогда, если воспользоваться формулой для силы vX В(не забудьте, что электрон отрицательный!), мы получим, что в соответствии с этим физическим законом электрон должен отклоняться в указанном направлении. Таким образом, явление заключается вот в чем. Если в катушке в определенном направлении течет ток, то электрон как-то отклоняется. Это и есть физика, и не­важно, как мы будем называть все по дороге.