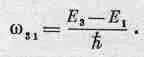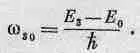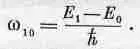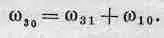Feynmann - Feynmann 3a

Фиг. 38.9. Схема энергий атома. Показано несколько возможных переходов .

Поэтому, например, частота света, освобожденного в переходе от энергии Е 3 к энергии E 1 , равна

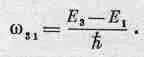
(38.14)

Эта частота характерна для данного сорта атомов и определяет линию в спектре испускания. Возможен и другой переход — от E 3к Е 0. У него своя частота:

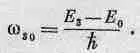
(38.15)

Еще одна возможность заключается в том, что если атом воз­бужден до состояния E 1, то он может упасть в основное состоя­ние е 0, излучая фотон с частотой

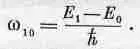
(38.16)

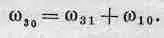
Мы привели здесь эти три перехода для того, чтобы подчеркнуть интересную связь между ними. Из трех формул (38.14), (38.15), (38.16) легко получить

(38.17)

Вообще, обнаружив две линии в спектре, можно ожидать, что найдется и линия с частотой, равной сумме (или разности) частот. Все линии можно объяснить, отыскав серию уровней, таких, что каждая линия соответствует разности энергий меж­ду какими-то двумя уровнями. Это замечательное совпадение между частотами линий в спектре было замечено еще до откры­тия квантовой механики. Его называют комбинационным прин­ципом Ритца. С точки зрения классической механики он опять выглядит таинственно. Впрочем, не будем больше напоминать о том, что классическая механика обанкротилась в мире ато­мов; мне кажется, мы это уже хорошо показали.

Мы говорили уже о том, что в квантовой механике все собы­тия представляются в виде амплитуд, которые ведут себя как волны, имеют определенную частоту и волновое число. Посмот­рим теперь, как при помощи амплитуд объяснить, что у атома бывают только определенные энергетические состояния. Из всего, что было сказано до сих пор, это вывести и понять невоз­можно. Но зато мы все знаем, что волны в ограниченном объеме обладают определенными частотами. Скажем, если звуковая волна ограничена пределами органной трубы или как-либо иначе, то звуковые колебания могут быть разными, но их ча­стоты не могут быть любыми. И так всегда: у тела, внутри которого держатся волны, всегда бывают определенные резонанс­ные частоты. Волны, заключенные в ограниченный объем, всег­да обладают лишь определенным набором частот. (В дальней­шем мы еще будем изучать это явление и выпишем все нужные формулы.) Ну, а поскольку существует общее соотношение между частотой колебаний амплитуды и энергией, то нет ниче­го удивительного в том, что электроны, связанные в атомах, обладают только вполне определенными энергиями.

§ 6. Немного философии

Поговорим еще немного о философии квантовой механики. Как и всегда, здесь есть две стороны: философское содержание физики и его экстраполяция на другие области знаний. Когда философские идеи, связанные с наукой, переносятся на другие области, они обычно при этом искажаются до неузнаваемости. Поэтому мы ограничим свои замечания, насколько это возмож­но, только физикой.

Прежде всего начнем с самого интересного предмета — с идеи принципа неопределенности: наблюдение воздействует на явле­ние. Хоть и всегда было известно, что, наблюдая явление, мы воздействуем на него, но здесь суть-то в том, что этим воздейст­вием нельзя пренебречь, нельзя его свести до нуля, нельзя переделкой прибора произвольно уменьшить это влияние. Наблюдая явление, нельзя хотя бы слегка не нарушить его ход, и без учета этого нарушения теория не может стать после­довательной. И в доквантовой физике наблюдатель иногда был важен, но лишь в довольно тривиальном смысле. Рассматривал­ся, скажем, такой вопрос: дерево падает в лесу, в котором нет никого, кто мог бы услышать это; вызовет ли падение шум? И следовал ответ: настоящее дерево, падая в настоящем лесу, бесспорно, шум вызовет, даже если никого поблизости нет. Пусть никто падения слышать не мог, все равно останутся другие следы — кое-где осыплются листья, а на некоторых листочках останутся едва заметные царапинки от колючек, которые можно будет объяснить лишь тем, что листва дро­жала. Так что следует допустить, что в некотором смысле звук и впрямь существовал. «Но было ли ощущение зву­ка?» — можем мы спросить. Нет, для ощущения, видимо, нуж­но и сознание. А есть ли сознание у муравьев, да и водятся ли они в этом лесу и сознают ли что-либо деревья — вопрос темный. Поэтому бросим эту задачу.