Feynmann - Feynmann 3

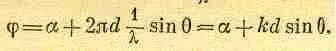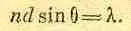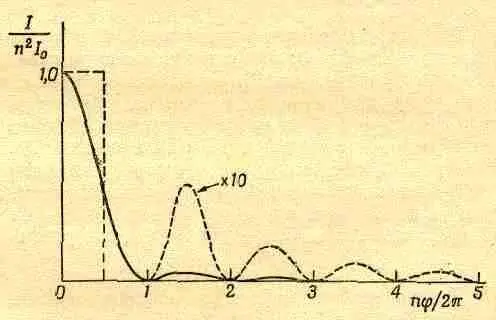
Фиг. 30. 2. Зависимость интенсивности от фазово­го угла для большого числа осцилляторов с одинаковыми амплитудами.

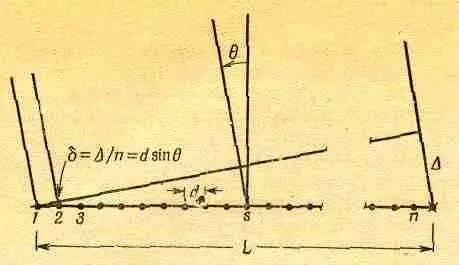
Фиг. 30 .3. Устройство из n одинаковых осцил­ляторов, расположенных на линии. Фаза колебания s-го осциллятора равна a s =sa.

Можно показать, что площадь под кривой интенсивности, включая все максимумы, равна 2pnI 0и в два раза превышает площадь пунктирного прямоугольника на фиг. 30.2.

Посмотрим теперь, что дает формула (30.3) в приложении к разным случаям. Пусть источники расположены на одной ли­нии, как показано на фиг. 30.3. Всего имеется n источников на расстоянии d друг от друга, и сдвиг фазы между соседними источ­никами выбран равным а. Тогда для лучей, распространяющихся в заданном направлении Э, отсчитываемом от нормали, вследст­вие разности хода лучей от двух соседних источников возникает

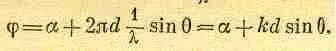
дополнительный сдвиг фазы 2pd(1/l)sinq. Таким образом,

(30.4)

Рассмотрим сначала случай a=0. Все осцилляторы колеб­лются с одной фазой; требуется найти интенсивность их излуче­ния как функцию угла В. Подставим с этой целью j = kdsin q в формулу (30.3) и посмотрим, что получится в результате. Пре­жде всего, при j=0 возникает максимум. Значит, осцилляторы, колеблющиеся с одной фазой, дают мощное излучение в направ­лении 0 =0. Интересно узнать, где находится первый минимум.

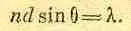
Он возникает при j=2p/n; другими словами, первый мини­мум кривой интенсивности определяется из соотношения (2pd/l)sinq =2 p / n . Сокращая на 2p, получаем

(30.5)

Теперь разберем с физической точки зрения, почему мини­мум возникает именно в этом месте. В этом выражении nd есть полная длина L нашей системы осцилляторов. Обращаясь к фиг. 30.3, мы видим, что ndsinq = L sinq=D. Формула (30.5) подсказывает нам, что минимум возникает при D, равном одной длине волны. Но почему минимум получается при D = l? Дело в том, что поля от отдельных осцилляторов равномерно распределены по фазе от 0 до 360°. Стрелки (см. фиг. 30.1) опи­сывают полную окружность; мы складываем равные векторы, имеющие произвольные направления, а в этом случае сумма равна нулю. Вот при таких значениях угла, когда D=l, воз­никает минимум. Это и есть первый минимум.

Формула (30.3) имеет еще одну важную особенность: при уве­личении угла j на число, кратное 2p, значение интенсивности не меняется. Поэтому для j =2p, 4p, 6p и т. д. также возникают резкие и высокие максимумы. Вблизи этих максимумов интен­сивность повторяет свой ход (см. фиг. 30.2). Зададимся вопро­сом, в силу каких геометрических соотношений возникают дру­гие максимумы? Условие появления максимума записывается в виде j==2pm, где m — любое целое число. Отсюда получаем (2pd/l)sinq=2pm. Сокращая на 2p, получаем

dsinq = m l . (30.6)

Это соотношение очень похоже на формулу (30.5). Однако там было nd sin q=l. Разница в том, что здесь нужно взять каж­дый отдельный источник и выяснить, что для него означает условие n dsin q = m l ; угол q здесь таков, что разность хода d =т l . Другими словами, волны, идущие от источников, раз­личаются по фазе на величину, кратную 360°, и, следовательно, все находятся в фазе. Поэтому при сложении волн возникает столь же высокий максимум, как и в рассмотренном ранее слу­чае т =0. Побочные максимумы и весь ход интенсивности здесь такие же, как в случае j =0. Таким образом, наша система посы­лает пучки лучей в разных направлениях, причем каждый пу­чок имеет высокий центральный максимум и ряд слабых боко­вых. Главные (центральные) максимумы в зависимости от вели­чины т называются максимумами нулевого, первого и т. д. порядков; т называют порядком максимума.

Обратите внимание на такой факт: если d меньше l , то фор­мула (30.6) имеет единственное решение при т =0. Поэтому для малого расстояния между источниками возникает один-един­ственный пучок, сконцентрированный около q=0. (Разумеется, есть еще пучок в обратном направлении.) Чтобы получить мак­симумы других порядков, расстояние d должно быть больше одной длины волны.